
【题目】全球最大的关公塑像矗立在荆州古城东门外.如图,张三同学在东门城墙上C处测得塑像底部B处的俯角为18°48′,测得塑像顶部A处的仰角为45°,点D在观测点C正下方城墙底的地面上,若CD=10米,则此塑像的高AB约为米(参考数据:tan78°12′≈4.8).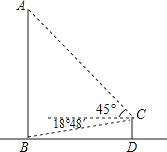
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】阅读下面的对话:
MM:“请帮我称些梨.”
售货员:“您上次买的梨卖没了,您试一试新进的苹果,价格虽然比梨贵些,但苹果营养价
值更高.”
MM:“好,我跟上次一样,也买30元钱.”
对比两次的电脑小票,MM发现:每千克苹果的价格是梨的1.5倍,苹果的重量比梨轻2.5
千克.
根据上面的对话和MM发现,分别求出苹果和梨的单价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y= ![]() x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点. 
(1)求抛物线的解析式;
(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在直角坐标系xoy中,直线l:y=kx+b交x轴,y轴于点E,F,点B的坐标是(2,2),过点B分别作x轴、y轴的垂线,垂足为A、C,点D是线段CO上的动点,以BD为对称轴,作与△BCD或轴对称的△BC′D.
(1)当∠CBD=15°时,求点C′的坐标.
(2)当图1中的直线l经过点A,且k=﹣ ![]() 时(如图2),求点D由C到O的运动过程中,线段BC′扫过的图形与△OAF重叠部分的面积.
时(如图2),求点D由C到O的运动过程中,线段BC′扫过的图形与△OAF重叠部分的面积.
(3)当图1中的直线l经过点D,C′时(如图3),以DE为对称轴,作于△DOE或轴对称的△DO′E,连结O′C,O′O,问是否存在点D,使得△DO′E与△CO′O相似?若存在,求出k、b的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个长为8分米,宽为5分米,高为7分米的长方体上,截去一个长为6分米,宽为5分米,深为2分米的长方体后,得到一个如图所示的几何体.一只蚂蚁要从该几何体的顶点A处,沿着几何体的表面到几何体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是 分米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的坐标系中,△ABC的三个顶点的坐标依次为A(﹣1,2),B(﹣4,1),C(﹣2,﹣2)
(1)请写出△ABC关于x轴对称的点A1、B1、C1的坐标;
(2)请在这个坐标系中作出△ABC关于y轴对称的△A2B2C2;
(3)计算:△A2B2C2的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com