
����Ŀ����2014����18�⣩ij��ȤС��Ϊ�˽ⱾУ�����μӿ���������������������ȡ��У300�������������ʾ����飬ͳ�����������������������в�������ͳ��ͼ��
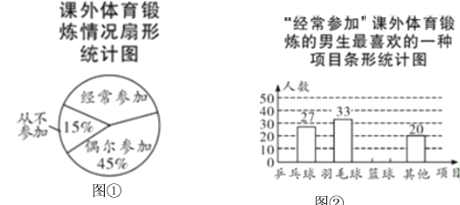
�����������Ϣ����������⣺
��1���������������������ͳ��ͼ�У��������μӡ�����Ӧ��Բ�ĽǵĶ���Ϊ________��
��2���벹ȫ����ͳ��ͼ��
��3����У����1200�������������ȫУ�����о����μӿ�����������������ϲ������Ŀ�������������
��4��С����Ϊ��ȫУ���������У�������ϲ���μӵ��˶���Ŀ��ƹ���������ԼΪ![]() ���������ж�����˵���Ƿ���ȷ����˵�����ɣ�
���������ж�����˵���Ƿ���ȷ����˵�����ɣ�
���𰸡�(1)144����(2)��ͼ��������(3)ȫУ1200�������о����μӿ�����������������ϲ������Ŀ�����������Լ��160�ˣ�(4)����ȷ�����ɼ�����
��������
(1)144����
[�ⷨ��ʾ]������ͳ��ͼ��֪���������μ�����ռ�İٷֱ�Ϊ��![]() �����������μ�������Ӧ��Բ�ĽǵĶ���Ϊ��
�����������μ�������Ӧ��Բ�ĽǵĶ���Ϊ��![]() ��
��
(2)��ȫ����ͳ��ͼ���ͼ��

[�ⷨ��ʾ]��(1)��֪���������μ�����ռ�İٷֱ�Ϊ40%�����������μ�����Ƶ��Ϊ��![]() (��)��������ͳ��ͼ��֪ϲ�����������Ϊ��
(��)��������ͳ��ͼ��֪ϲ�����������Ϊ��![]() (��)��
(��)��
(3)![]() (��)��
(��)��
��ȫУ1200�������о����μӿ�����������������ϲ������Ŀ�����������Լ��160�ˣ�
(4)����ȷ��
���ɣ���С���ǰ����������ȫУ����������ϲ��ƹ�����˶�������������![]() ����������300��ѧ���о����μӿ�����������������ϲ��ƹ������Ŀ��������ռ��Ƶ������������ȫУ����������ϲ��ƹ������Ŀ��������ռ��Ƶ�ʣ�ȫУ1200�������У�ż���μӿ�������������������Ҳ������ϲ��ƹ�����˶��ģ�����С����˵������ȷ��
����������300��ѧ���о����μӿ�����������������ϲ��ƹ������Ŀ��������ռ��Ƶ������������ȫУ����������ϲ��ƹ������Ŀ��������ռ��Ƶ�ʣ�ȫУ1200�������У�ż���μӿ�������������������Ҳ������ϲ��ƹ�����˶��ģ�����С����˵������ȷ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ������չ��������������������������������������ܲ������˶���Ŀ��Ϊ�˽�ѧ����ϲ����һ����Ŀ�������ȡ�˲���ѧ�����е��飬�����������µ�����ͳ��ͼ������ͳ��ͼ��������Ϣδ��������
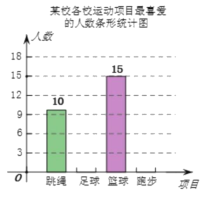
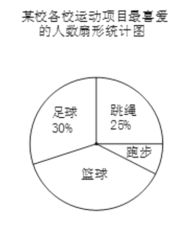
��1���α������ѧ��������
��2����ȫ����ͳ��ͼ��
��3��������ͳ��ͼ�У�������������Ӧ��Բ�ĽǶ���Ϊ__ ��
��4����У����3000��ѧ���������ȫУ��ϲ���������������ϲ���������������٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
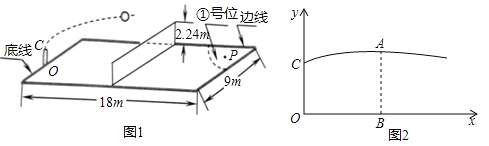
����Ŀ����ͼ1������Ϊ18m����Ϊ9m������Ϊ2.24m����Ավ�ڵ���O�㴦������ӵ�O�����Ϸ�1.9m��C�㷢�����˶�·���������ߵ�һ���֣������˶�����ߵ�Aʱ���߶�Ϊ2.88m����BA��2.88m����ʱˮƽ����OB��7m����ֱ��OBΪx�ᣬֱ��OCΪy�ᣬ����ƽ��ֱ������ϵ����ͼ2��
��1����������ǰ���˶�����x�ᴹֱ�ڵ��ߣ��������˶��ĸ߶�y��m����ˮƽ����x��m��֮��ĺ�����ϵʽ������д��xȡֵ��Χ�������ж���η����ܷ�������Ƿ���磿˵�����ɣ�
��2����������������ǶԷ���������λ�ڵĵ�P����ͼ1����P�����1m������0.5m�����ʷ����O�ڵ����ϵ��ĸ�λ�ã����ο����ݣ�![]() ȡ1.4��
ȡ1.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���![]() ��
��![]() ��
��![]() ������
������![]() ����
����![]() ������
������![]() �ϣ���
�ϣ���![]() Ϊ����
Ϊ����![]() �Ϸ���
�Ϸ���![]() ����
����![]() ������
������![]() ��
��
��1������![]() ���߶�
���߶�![]() ��ʱ��֤����
��ʱ��֤����![]() ��
��
��2����![]() ʱ����
ʱ����![]() �������
�������
��3��![]() �����Բ������
�����Բ������![]() �ڵ�
�ڵ�![]() ����ֱ��
����ֱ��![]() ��ֱ��
��ֱ��![]() �ڵ�
�ڵ�![]() ����ֱ��
����ֱ��![]() �ڵ�
�ڵ�![]() ������
������![]() ����
����![]() �����߶�
�����߶�![]() �ij���
�ij���
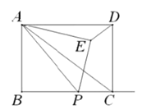
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������κ���y=ax2+bx+c��ͼ����x�������������㣬��ôһԪ���η���ax2+bx+c=0����������ȵ�ʵ������������������仰�����⣬����������⣺��m��n��m��n���ǹ���x�ķ���1����x��a����x��b��=0����������a��b����a��b��m��n�Ĵ�С��ϵ�ǣ� ����
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������һ��ֱ��Ϊ16��Բ����ˮ�أ���ˮ�ص��ܱ���һȦ��ˮͷ�������ˮ��Ϊ�����ߣ��ھ�ˮ������3�״��ﵽ��ߣ��߶�Ϊ5�ף��Ҹ����������ˮ��ǡ������ˮ�����ĵ�װ���ﴦ��ϣ���ͼ��ʾ����ˮƽ����Ϊx�ᣬ��ˮ������Ϊԭ�㽨��ֱ������ϵ��
��1����ˮ�����������ߣ���һ�����֣��ĺ�������ʽ��
��2����ʦ������ˮ����ά���豸�ڼ䣬��ˮ��������ˮ��Ϊ�˲�����ʪ������1.8����ʦ��վ��ʱ��������ˮ�����Ķ��������ڣ�
��3��������������������������ˮ��ʩ��������ƸĽ��������ˮ������״�����ǰ���£���ˮ�ص�ֱ������32�ף������������ˮ��������ˮ�����ı�����ԭװ����߶Ȳ��䣩����ϣ���̽�������������ˮ��ˮ�������߶ȣ�

�鿴�𰸺ͽ���>>
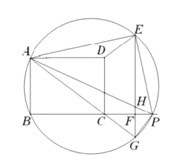
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С������12�֣�
��֪����Rt��ABC��Rt��DEF����ͼ��1���ڷţ���C���E�غϣ�����B��C��E����F��ͬһ��ֱ���ϣ���ACB = ��EDF = 90�㣬��DEF = 45����AC = 8 cm��BC = 6 cm��EF = 9 cm��
��ͼ��2������DEF��ͼ��1����λ�ó�������1 cm/s���ٶ���CB����ABC��������������DEF������ͬʱ����P����ABC�Ķ���B��������2 cm/s���ٶ���BA���A��������.����DEF�Ķ���D�ƶ���AC����ʱ����DEFֹͣ��������PҲ��ֹ֮ͣ�ƶ���DE��AC�ཻ�ڵ�Q������PQ��������ʱ��Ϊt��s����0��t��4.5����

����������⣺
��1����tΪ��ֵʱ����A���߶�PQ�Ĵ�ֱƽ�����ϣ�
��2������PE�����ı���APEC�����Ϊy��cm2������y��t֮��ĺ�����ϵʽ���Ƿ����ijһʱ��t��ʹ���y��С�������ڣ����y����Сֵ���������ڣ�˵�����ɣ�
��3���Ƿ����ijһʱ��t��ʹP��Q��F������ͬһ��ֱ���ϣ������ڣ������ʱt��ֵ���������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ1��ijС�������IJ���ʾ��ͼ�����о���![]() ��ʾ�ó��ĺ��䣬�ڴ���Ĺ����У����
��ʾ�ó��ĺ��䣬�ڴ���Ĺ����У����![]() �����Ƶ�
�����Ƶ�![]() ��ʱ�뷽����ת������ת��Ϊ
��ʱ�뷽����ת������ת��Ϊ![]() ʱ�����
ʱ�����![]() ����
����![]() ��λ�ã�������Ŵ����ͼ2��ʾ������֪
��λ�ã�������Ŵ����ͼ2��ʾ������֪![]() ���ף�
���ף�![]() ���ף�
���ף�![]() ���ף���ͼ2����
���ף���ͼ2����

��1����![]() ��
��![]() �ľ��루����������ţ���
�ľ��루����������ţ���
��2��![]() ��
��![]() ����ľ��루����������ţ���
����ľ��루����������ţ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵ�У�������y=��x2��2![]() x�Ķ���ΪA�㣬����x��������ύ�ڵ�B��P��Ϊ�������߶Գ�����һ�㣬��OP��
x�Ķ���ΪA�㣬����x��������ύ�ڵ�B��P��Ϊ�������߶Գ�����һ�㣬��OP��![]() AP����СֵΪ�� ��.
AP����СֵΪ�� ��.
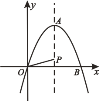
A. 3 B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com