
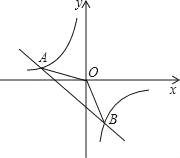
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A(﹣2,1),B(1,n).
的图象交于A(﹣2,1),B(1,n).
(1)试确定上述反比例函数和一次函数的表达式;
(2)求△ABO的面积;
(3)根据图象写出使反比例函数的值大于一次函数值的自变量x的取值范围.
【答案】(1)y=-![]() ,y=-x-1(2)1.5(3)﹣2<x<0或x>1
,y=-x-1(2)1.5(3)﹣2<x<0或x>1
【解析】试题分析:(1)待定系数法求函数表达式.(2)三角形面积公式求解.(3)根据图象的高低求出范围.
试题解析:
(1)∵把A(﹣2,1)代入y=![]() 得:m=﹣2,
得:m=﹣2,
∴反比例函数的解析式是y=﹣![]() .
.
∵把B(1,n)代入反比例函数y=﹣![]() 得:n=﹣2,
得:n=﹣2,
∴B的坐标是(1,﹣2),
把A、B的坐标代入一次函数y=kx+b得: ![]() ,
,
解得:k=﹣1,b=﹣1,
∴一次函数的解析式是y=﹣x﹣1;
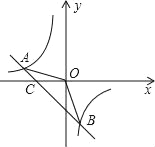
(2)设一次函数与x轴交于点C.
把y=0代入y=﹣x﹣1,得:0=﹣x﹣1,交点x=﹣1,
∴C(﹣1,0),
∴△AOB的面积=SAOC+S△BOC=![]() ×|﹣1|×1+
×|﹣1|×1+![]() ×|﹣1|×|﹣2|=1.5;
×|﹣1|×|﹣2|=1.5;
(3)从图象可知:当反比例函数的值大于一次函数值时x的取值范围﹣2<x<0或x>1.


 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】在一条直路上的![]() 、
、![]() 、
、![]() 、
、![]() 四个车站的位置如图所示(单位千米),如果小明家在
四个车站的位置如图所示(单位千米),如果小明家在![]() 站旁,他的同学小亮家在
站旁,他的同学小亮家在![]() 站旁,新华书店在
站旁,新华书店在![]() 站旁,一天小明乘车从
站旁,一天小明乘车从![]() 站出发到
站出发到![]() 站下车去新华书店购买一些课外阅读书籍,途径
站下车去新华书店购买一些课外阅读书籍,途径![]() 、
、![]() 两站,当小明到达
两站,当小明到达![]() 站时发现自己所带钱不够购买自己所要的书籍.于是他乘车返回到
站时发现自己所带钱不够购买自己所要的书籍.于是他乘车返回到![]() 站处下车向小亮借足了钱,然后乘车继续赶往
站处下车向小亮借足了钱,然后乘车继续赶往![]() 站旁的新华书店.
站旁的新华书店.
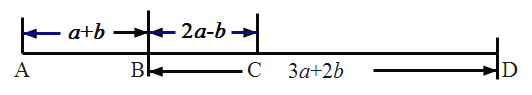
(1)求![]() 、
、![]() 两站的距离;(用含有
两站的距离;(用含有![]() 、
、![]() 的代数式表示)
的代数式表示)
(2)求这一天小明从![]() 站到
站到![]() 站乘车路程.(用含有
站乘车路程.(用含有![]() 、
、![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强打算找印刷公司设计一款新年贺卡并印刷.如图1是甲印刷公司设计与印刷卡片计价方式的说明(包含设计费与印刷费),乙公司的收费与印刷卡片数量的关系如图2所示.
(1)分别写出甲乙两公司的收费y(元)与印刷数量x之间的关系式.
(2)如果你是小强,你会选择哪家公司?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E,F分别为AD,BC边上的一点,增加下列条件,不能得出BE∥DF的是( )

A. AE=CF B. BE=DF C. ∠EBF=∠FDE D. ∠BED=∠BFD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
(1)求抛物线的解析式;
(2)试探究△ABC的外接圆的圆心位置,并求出圆心坐标;
(3)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△BAC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′,若∠CC′B′=30°,求∠B的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+
x+![]() 分别与x轴、y轴交于B,C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+
分别与x轴、y轴交于B,C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+![]() 经过A,B两点,A点坐标为(﹣1,0).
经过A,B两点,A点坐标为(﹣1,0).
(1)求B、C两点的坐标;
(2)求抛物线的解析式;
(3)点M是直线BC上方抛物线上的一点,过点M作MH⊥BC于点H,作MD∥y轴交BC于点D,求△DMH周长的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形ABCD,E为平面内任意一点,连接DE,将线段DE绕点D顺时针旋转90°得到DG,连接EC,AG.
(1)当点E在正方形ABCD内部时,
①根据题意,在图1中补全图形;
②判断AG与CE的数量关系与位置关系并写出证明思路.
(2)当点B,D,G在一条直线时,若AD=4,DG=![]() ,求CE的长.(可在备用图中画图)
,求CE的长.(可在备用图中画图)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级甲,乙两班各有![]() 名学生,为了解这两个班学生身体素质情况,进行了抽样调查.从这两个班各随机抽取
名学生,为了解这两个班学生身体素质情况,进行了抽样调查.从这两个班各随机抽取![]() 名学生进行身体素质测试,测试成绩如下:
名学生进行身体素质测试,测试成绩如下:
甲班![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
乙班![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
整理上面数据,得到如下统计表:

样本数据的平均数、众数.中位数如下表所示:
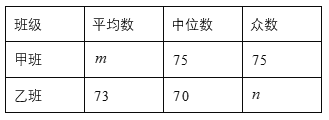
根据以上信息,解答下列问题:
(1)求表中![]() 的值
的值
(2)表中![]() 的值为( )
的值为( )
(3)若规定测试成绩在![]() 分以上(含
分以上(含![]() 分)的学生身体素质为优秀,请估计乙班
分)的学生身体素质为优秀,请估计乙班![]() 名学生中身体素质为优秀的学生的人数.
名学生中身体素质为优秀的学生的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com