
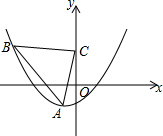
 已知,抛物线y=$\frac{1}{8}$(x+1)2-2顶点为A,点B在抛物线上,以AB的斜边作等腰直角三角形,直角顶点C在y轴上,求C点坐标.
已知,抛物线y=$\frac{1}{8}$(x+1)2-2顶点为A,点B在抛物线上,以AB的斜边作等腰直角三角形,直角顶点C在y轴上,求C点坐标. 分析 由抛物线的顶点式求得A的坐标,作BE⊥y轴于E,AF⊥y轴于F,根据等腰直角三角形的性质得出AC=BC,∠ACF=∠EBC,然后证得△ACF≌△CBE,得出AF=CE,CF=BE,设C(0,n),则BE=CF=n+2,AF=CE=1,得出B(-n-2,n+1),代入抛物线的解析式即可求得.
解答 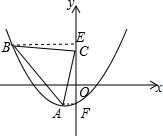 解:∵抛物线y=$\frac{1}{8}$(x+1)2-2顶点为A,
解:∵抛物线y=$\frac{1}{8}$(x+1)2-2顶点为A,
∴A(-1,-2),
作BE⊥y轴于E,AF⊥y轴于F,
∵△ABC是以AB的斜边等腰直角三角形,
∴AC=BC,∠ACB=90°,
∴∠BCE+∠ACF=90°,
∵∠BCE+∠EBC=90°,
∴∠ACF=∠EBC,
在△ACF和△CBE中
$\left\{\begin{array}{l}{∠ACF=∠EBC}\\{∠AFC=∠CEB=90°}\\{AC=BC}\end{array}\right.$
∴△ACF≌△CBE(AAS),
∴AF=CE,CF=BE,
设C(0,n),则BE=CF=n+2,AF=CE=1,
∴B(-n-2,n+1),
∵点B在抛物线上,
∴n+1=$\frac{1}{8}$(-n-2+1)2-2,
解得n=3±4$\sqrt{2}$,
∴C(0,3+4$\sqrt{2}$)或(0,3-4$\sqrt{2}$).
点评 本题考查了二次函数的性质,二次函数图象上点的坐标特征,等腰直角三角形的性质,三角形全等的判定和性质,作出辅助线构建全等三角形是解题的关键.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
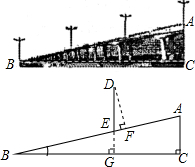 如图是某城市一座立交桥的引桥部分,桥面截面AB可以近似地看做Rt△ABC的斜边,桥面AB上路灯DE的高度为5m,已知坡角∠ABC为14°,求路灯DE的顶端D点到桥面AB的垂直距离(即DF的长,精确到0.1m).
如图是某城市一座立交桥的引桥部分,桥面截面AB可以近似地看做Rt△ABC的斜边,桥面AB上路灯DE的高度为5m,已知坡角∠ABC为14°,求路灯DE的顶端D点到桥面AB的垂直距离(即DF的长,精确到0.1m).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
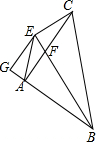 如图,△ABC中,AB=AC,∠BAC=90°,BE平分∠ABC交AC于F,CE⊥BF于E,EG⊥AB于G,连AE.下列结论:①AB+AF=BC;②BF=2CE;③FC=GE;④∠GEA=∠CBF.其中正确的有( )
如图,△ABC中,AB=AC,∠BAC=90°,BE平分∠ABC交AC于F,CE⊥BF于E,EG⊥AB于G,连AE.下列结论:①AB+AF=BC;②BF=2CE;③FC=GE;④∠GEA=∠CBF.其中正确的有( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
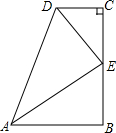 在数学活动课上,小明提出这样一个问题:如右图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB的度数是( )
在数学活动课上,小明提出这样一个问题:如右图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB的度数是( )| A. | 65° | B. | 55° | C. | 45° | D. | 35° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com