
����Ŀ���涨���������x��һԪ���η���ax2+bx+c��0��a��0��������ʵ������������һ��������һ������2������������ķ���Ϊ�������������������н���
�ٷ���x2+2x��8��0�DZ������̣�
��������x�ķ���x2+ax+2��0�DZ������̣���a����3��
������x��3����mx��n����0�DZ������̣���n��6m��3n��2m��
�����㣨m��n���ڷ���������y��![]() ��ͼ���ϣ������x�ķ���mx2��3x+n��0�DZ������̣�
��ͼ���ϣ������x�ķ���mx2��3x+n��0�DZ������̣�
������������ȷ���У�������
A. �٢�B. �ۢ�C. �ڢ�D. �ڢ�
���𰸡�D
��������
����ͨ���ⷽ�̵õ��÷��̵ĸ�������������������Ķ�������жϣ�
����x2=2x1���õ�x1x2=2x12=2���õ���x1=1ʱ��x2=2����x1=-1ʱ��x2=-2�����ǵõ����ۣ�
�۸����������������Ķ��弴�ɵõ����ۣ�
�����㣨m��n���ڷ���������y��![]() ��ͼ���ϣ��õ�mn=2��Ȼ��ⷽ��mx2-3x+n=0���ɵõ���ȷ�Ľ��ۣ�
��ͼ���ϣ��õ�mn=2��Ȼ��ⷽ��mx2-3x+n=0���ɵõ���ȷ�Ľ��ۣ�
�⣺�١߷���x2+2x-8=0����������x1=-4��x2=2����2��2��-4��
���x2+2x-8=0���DZ������̣��ʢٴ���
��������x�ķ���x2+ax+2=0�DZ������̣���2x1=x2��
��x1+x2=-a��x1x2=2��
��2x12=2�����x1=��1��
��x2=��2��
��a=��3���ʢ���ȷ��
�۽ⷽ�̣�x-3����mx-n��=0�ã�![]() ��
��
����x-3����mx-n��=0�DZ������̣���![]() ��
��![]() ��
��
��n=6m��3m=2n���ʢ۴���
�ܡߵ㣨m��n���ڷ���������y��![]() ��ͼ���ϣ�
��ͼ���ϣ�
��mn=2����![]() ��
��
�����x�ķ���Ϊ![]() ��
��
�ⷽ�̵�![]() ��
��
��x2=2x1��
�����x�ķ���mx2-3x+n=0�DZ������̣��ʢ���ȷ��
��ѡ��D��


 ���ٴ�����ɽ����ϵ�д�
���ٴ�����ɽ����ϵ�д� ���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�
���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABCD�У���BAD��ƽ���߽�ֱ��BC�ڵ�E����ֱ��DC���ӳ����ڵ�F����EC��CFΪ�ڱ���ECFG.
(1)��ͼ1��֤��ECFGΪ���Σ�
(2)��ͼ2,����ABC=120��,����BG��CG,�������BDG�Ķ�����
(3)��ͼ3,����ABC=90����AB=6,AD=8,M��EF���е㣬��DM�ij�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һԪ���η���ax2+bx+c=0��a��0���У�����˵����
����a+b+c=0����b2��4ac��0��
��������������1��2����2a+c=0��
��������ax2+c=0����������ȵ�ʵ������ax2+bx+c=0������������ȵ�ʵ����
����b=2a+c��������������ȵ�ʵ����������ȷ���У�������
A. �٢ڢ� B. �٢ڢ� C. �ڢۢ� D. �٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��y��![]() x��4��x�ᡢy��ֱ��ڵ�A�͵�B����C��D�ֱ�Ϊ�߶�AB��OB���е㣬��PΪOA��һ���㣬PC��PDֵ��Сʱ��P������Ϊ.
x��4��x�ᡢy��ֱ��ڵ�A�͵�B����C��D�ֱ�Ϊ�߶�AB��OB���е㣬��PΪOA��һ���㣬PC��PDֵ��Сʱ��P������Ϊ.

A. (��3��0) B. (��6��0) C. (��![]() ��0) D. (��
��0) D. (��![]() ��0)
��0)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�����ߵĶ���ΪP��1��4������������y�ύ�ڵ�C��0��3������x�ύ��A��B���㣮
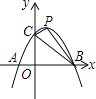
��1����������ߵĽ���ʽ��
��2�����ı���OBPC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�D��E�ֱ���AB��AC���е㣬BE��2DE���ӳ�DE����F��ʹ��EF��BE������CF��
��1����֤���ı���BCFE�����Σ�
��2����CE��2����BCF��120����������BCFE�������
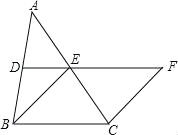
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2016�꣬ijƶ�����ļ�ͥ���˾�������Ϊ2500Ԫ��ͨ��������ҵ���֣���չ����ֳҵ��2018�꣬��ͥ���˾�������ﵽ��3600Ԫ��
��1�����ƶ����2016�굽2018���ͥ���˾����������ƽ�������ʣ�
��2������ƽ�������ʱ��ֲ��䣬2019���ƶ�����ļ�ͥ���˾��������Ƿ��ܴﵽ4200Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��ͬѧ���ۺ�ʵ����жԱ��ص�һ�����������˲�������ͼ������ɽ���½�P����ù�������M������Ϊ![]() ����ɽ��������25m����D������ù�������M������Ϊ
����ɽ��������25m����D������ù�������M������Ϊ![]() ����֪ɽ���¶�
����֪ɽ���¶�![]() ����
����![]() ���������С����������ĸ߶�ME���������ȷ��0.1m���ο����ݣ�
���������С����������ĸ߶�ME���������ȷ��0.1m���ο����ݣ�![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB��90��������ABC�ƶ���C��ʱ����ת�õ���A��B��C��M��BC���е㣬P��A��B�����е㣬����PM����BC��2����BAC��30�������߶�PM�����ֵ��_____��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com