
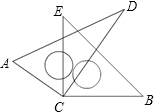
如图,将两块直角三角尺的直角顶点C叠放在一起.
(1)判断∠ACE与∠BCD的大小关系,并说明理由;
(2)若∠DCE=30°,求∠ACB的度数;
(3)猜想:∠ACB与∠DCE有怎样的数量关系,并说明理由.
【考点】余角和补角.
【分析】(1)根据余角的性质,可得答案;
(2)根据余角的定义,可得∠ACE,根据角的和差,可得答案;
(3)根据补角的定义,可得答案.
【解答】解:(1)∠ACE=∠BCD,理由如下:
∵∠ACE+∠DCE=90°,∠BCD+∠DCE=90°,
∴∠ACE=∠BCD;
(2)由余角的定义,得∠ACE=90°﹣∠DCE=90°﹣30°=60°,
由角的和差,得∠ACB=∠ACE+∠BCE=60°+90°=150°;
(3)∠ACB+∠DCE=180°,理由如下:
由角的和差,得∠ACB=∠BCE+∠ACE,
∠ACB+∠DCE=∠BCE+(∠ACE+DCE)=∠BCE+∠ACE=180°.
【点评】本题考查了余角和补角,利用了余角的性质,补角的性质,角的和差.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
如图,已知FG⊥AB,CD⊥AB,垂足分别为G、D,∠1=∠2,
求证:∠CED+∠ACB=180°.请你将小明的证明过程补充完整.
证明:∵FG⊥AB,CD⊥AB,垂足分别为G、D(已知)
∴∠FGB=∠CDB=90°( ),
∴GF∥CD ( ).
∵GF∥CD(已证)
∴∠2=∠BCD ( )
又∵∠1=∠2(已知),
∴∠1=∠BCD ( ),
∴ ,( )
∴∠CED+∠ACB=180° .


查看答案和解析>>
科目:初中数学 来源: 题型:
某班共有41名同学,其中有2名同学习惯用左手写字,其余同学都习惯用右手写字,老师随机请1名同学解答问题,习惯用左手写字的同学被选中的概率是( )
A.0 B.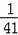
 C.
C.
 D.1
D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com