
如图,已知FG⊥AB,CD⊥AB,垂足分别为G、D,∠1=∠2,
求证:∠CED+∠ACB=180°.请你将小明的证明过程补充完整.
证明:∵FG⊥AB,CD⊥AB,垂足分别为G、D(已知)
∴∠FGB=∠CDB=90°( ),
∴GF∥CD ( ).
∵GF∥CD(已证)
∴∠2=∠BCD ( )
又∵∠1=∠2(已知),
∴∠1=∠BCD ( ),
∴ ,( )
∴∠CED+∠ACB=180° .


【考点】平行线的判定与性质.
【专题】推理填空题.
【分析】由FG⊥AB,CD⊥AB,得到∠FGB=∠CDB=90°,根据平行线的判定和性质得到∠2=∠BCD 由等量代换得到∠1=∠BCD,证出DE∥BC,从而证得结论.
【解答】证明:∵FG⊥AB,CD⊥AB,垂足分别为G、D(已知)
∴∠FGB=∠CDB=90°( 垂直的定义),
∴GF∥CD ( 同位角相等,两直线平行).
∵GF∥CD(已证)
∴∠2=∠BCD ( 两直线平行,同位角相等)
又∵∠1=∠2(已知),
∴∠1=∠BCD ( 等量代换),
∴DE∥BC,(内错角相等,两直线平行)
∴∠CED+∠ACB=180.(两直线平行,同旁内角互补)
故答案为:垂直的定义;同位角相等,两直线平行;两直线平行,同位角相等;等量代换;DE∥BC;内错角相等,两直线平行;两直线平行,同旁内角互补.
【点评】本题考查了平行线的判定与性质,属于基础题,关键是正确利用平行线的性质与判定定理证明.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
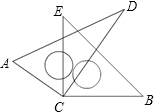
如图,将两块直角三角尺的直角顶点C叠放在一起.
(1)判断∠ACE与∠BCD的大小关系,并说明理由;
(2)若∠DCE=30°,求∠ACB的度数;
(3)猜想:∠ACB与∠DCE有怎样的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,两个直角三角形重叠在一起,将其中一个三角形沿着BC边平移到△DEF的位置,∠B=90°,AB=10,DH=2,平移距离为3,则阴影部分的面积为( )
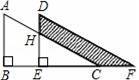

A.20 B.24 C.27 D.36
查看答案和解析>>
科目:初中数学 来源: 题型:
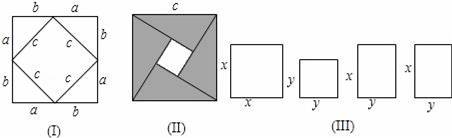
我们运用图(I)图中大正方形的面积可表示为(a+b)2,也可表示为c2+4×
 ab,即(a+b)2=c2+4×
ab,即(a+b)2=c2+4×
 ab由此推导出一个重要的结论a2+b2=c2,这个重要的结论就是著名的“勾股定理”.这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”.
ab由此推导出一个重要的结论a2+b2=c2,这个重要的结论就是著名的“勾股定理”.这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”.
(1)请你用图(Ⅱ)(2002年国际数字家大会会标)的面积表达式验证勾股定理(其中四个直角三角形的较大的直角边长都为a,较小的直角边长都为b,斜边长都为c).
(2)请你用(Ⅲ)提供的图形进行组合,用组合图形的面积表达式验证:(x+y)2=x2+2xy+y2
(3)现有足够多的边长为x的小正方形,边长为y的大正方形以及长为x宽为y的长方形,请你自己设计图形的组合,用其面积表达式验证:(x+y)(x+2y)=x2+3xy+2y2.

查看答案和解析>>
科目:初中数学 来源: 题型:
.一艘船从甲码头顺流而行,用了2小时到达乙码头,该船从乙码头返回甲码头逆流而行,用了2.5小时,已知水流速度是3千米/小时,则船在静水中的速度是 千米/小时.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com