
如图,两个直角三角形重叠在一起,将其中一个三角形沿着BC边平移到△DEF的位置,∠B=90°,AB=10,DH=2,平移距离为3,则阴影部分的面积为( )
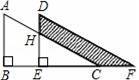

A.20 B.24 C.27 D.36
C【考点】平移的性质.
【分析】先根据图形平移的性质得出△ABC≌△DEF,故图中阴影部分的面积与梯形ABEH的面积相等,根据梯形的面积公式即可得出结论.
【解答】解:∵△DEF由△ABC平移而成,
∴△ABC≌△DEF,
∴图中阴影部分的面积与梯形ABEH的面积相等,
∵AB=10,DH=2,
∴EH=DE﹣DH=AB﹣DH=10﹣2=8,
∵BE=3,
∴S阴影=S梯形ABEH=
 (EH+AB)•BE=
(EH+AB)•BE=
 (10+8)×3=27.
(10+8)×3=27.
故选C.
【点评】本题考查的是平移的性质,熟知把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同是解答此题的关键.


科目:初中数学 来源: 题型:
如图,已知FG⊥AB,CD⊥AB,垂足分别为G、D,∠1=∠2,
求证:∠CED+∠ACB=180°.请你将小明的证明过程补充完整.
证明:∵FG⊥AB,CD⊥AB,垂足分别为G、D(已知)
∴∠FGB=∠CDB=90°( ),
∴GF∥CD ( ).
∵GF∥CD(已证)
∴∠2=∠BCD ( )
又∵∠1=∠2(已知),
∴∠1=∠BCD ( ),
∴ ,( )
∴∠CED+∠ACB=180° .


查看答案和解析>>
科目:初中数学 来源: 题型:
某班共有41名同学,其中有2名同学习惯用左手写字,其余同学都习惯用右手写字,老师随机请1名同学解答问题,习惯用左手写字的同学被选中的概率是( )
A.0 B.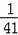
 C.
C.
 D.1
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
某公司生产一种产品,每件产品成本价是400元,销售价为510元,第一季度销售了5000件.
(1)求该产品第一季度的销售总利润(销售利润=销售价﹣成本价)是多少元?
(2)为进一步扩大市场,公司决定降低生产成本,经过市场凋研,在降低生产成本后,第二季度这种产品每件销售价降低了4%,销售量比第一季度提高了10%,销售总利润比第一季度提高了20%.求该产品每件的成本价降低了多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com