练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知关于x、y的二元一次方程kx﹣2y=4的解是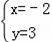，则k=　


    ﹣5　．

    【考点】二元一次方程的解．

    【分析】把方程的解代入方程求出k的值即可．

    【解答】解：把x=﹣2，y=3代入kx﹣2y=4，

    解得：k=﹣5．

    故答案为：﹣5．

    【点评】本题考查的是方程的解的概念，使方程两边的值相等的未知数的值是方程的解，解答此类题目时，把方程的解代入方程求值即可．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    老师带着两名学生到离学校33千米远的博物馆参观．老师乘一辆摩托车，速度25千米/小时．这辆摩托车后座可带乘一名学生，带人后速度为20千米/小时．学生步行的速度为5千米/小时．请你设计一种方案，使师生三人同时出发后都到达博物馆的时间不超过3小时．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    一个三角形的两条边长度分别为1和4，则第三边a可取　　．（填一个满足条件的数）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    计算﹣a2•（﹣6ab）的结果正确的是（　　）

    A．﹣2a3b      B．2a3b  C．﹣2a2b      D．2a2b

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，两个直角三角形重叠在一起，将其中一个三角形沿着BC边平移到△DEF的位置，∠B=90°，AB=10，DH=2，平移距离为3，则阴影部分的面积为（　　）

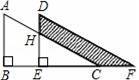
    A．20     B．24     C．27     D．36

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    x（x﹣y）﹣（x+2y）（2x﹣y）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


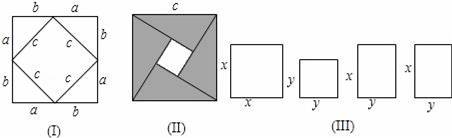
    我们运用图（I）图中大正方形的面积可表示为（a+b）2，也可表示为c2+4×ab，即（a+b）2=c2+4×ab由此推导出一个重要的结论a2+b2=c2，这个重要的结论就是著名的“勾股定理”．这种根据图形可以极简单地直观推论或验证数学规律和公式的方法，简称“无字证明”．

    （1）请你用图（Ⅱ）（2002年国际数字家大会会标）的面积表达式验证勾股定理（其中四个直角三角形的较大的直角边长都为a，较小的直角边长都为b，斜边长都为c）．

    （2）请你用（Ⅲ）提供的图形进行组合，用组合图形的面积表达式验证：（x+y）2=x2+2xy+y2

    （3）现有足够多的边长为x的小正方形，边长为y的大正方形以及长为x宽为y的长方形，请你自己设计图形的组合，用其面积表达式验证：（x+y）（x+2y）=x2+3xy+2y2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，AB为⊙O的直径，弦CD⊥AB，E为上一点，若∠CEA=28°，则∠ABD=　度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    ．已知m是方程2x2﹣5x﹣2=0的一个根，则代数式2m2﹣5m的值等于（　　）

    A．﹣2   B．0       C．1       D．2

    　

    查看答案和解析>>

    同步练习册答案