
【题目】如图,△ABC是⊙O的内接三角形,∠BAC的角平分线AE交⊙O于点E,交BC于点D,过点E作直线l∥BC.
(1)判断直线l与⊙O的位置关系,并说明理由;
(2)若在AE上取一点F使EF=BE,求证:BF是∠ABC的平分线;
(3)在(2)的条件下,若DE=3,BE=5,求AE的长.

【答案】(1)直线l与⊙O相切,见解析;(2)见解析;(3)AE=![]() .
.
【解析】
(1)连接OE,由AE平分∠BAC知![]() =
=![]() ,据此得OE⊥BC,根据l∥BC可得OE⊥l,从而得证;
,据此得OE⊥BC,根据l∥BC可得OE⊥l,从而得证;
(2)由BE=EF知∠EBF=∠EFB,由∠EFB=∠BAE+∠ABF、∠EBF=∠CBE+∠CBF及∠CBE=∠CAE=∠BAE可得∠ABF=∠CBF,从而得证;
(3)证△BED∽△AEB得![]() =
=![]() ,据此可得答案.
,据此可得答案.
(1)直线l与⊙O相切,
如图1,连接OE,
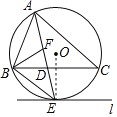
∵AE平分∠BAC,
∴∠BAE=∠CAE,
∴![]() =
=![]() ,
,
∴半径OE⊥BC,
∵l∥BC,
∴OE⊥l,
∴直线l与⊙O相切;
(2)∵BE=EF,
∴∠EBF=∠EFB,
∵∠EFB=∠BAE+∠ABF,∠EBF=∠CBE+∠CBF,
∴∠CBE+∠CBF=∠BAE+∠ABF,
∵∠CBE=∠CAE=∠BAE,
∴∠ABF=∠CBF,
∴BF平分∠ABC;
(3)∵∠DBE=∠BAE,∠DEB=∠BEA,
∴△BED∽△AEB,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得:AE=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】王勇和李明两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们共做了30次实验,实验的结果如下:
朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 2 | 5 | 6 | 4 | 10 | 3 |
(1)分别计算这30次实验中“3点朝上”的频率和“5点朝上”的频率;
(2)王勇说:“根据以上实验可以得出结论:由于5点朝上的频率最大,所以一次实验中出现5点朝上的概率最大”;李明说:“如果投掷300次,那么出现6点朝上的次数正好是30次”.试分别说明王勇和李明的说法正确吗?并简述理由;
(3)现王勇和李明各投掷一枚骰子,请用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
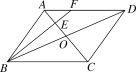
【题目】如图,在ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①![]() =
=![]() ;②S△BCE=36;③S△ABE=12;④△AEF∽△ACD,其中正确结论是_________.(把正确结论的序号都填上)
;②S△BCE=36;③S△ABE=12;④△AEF∽△ACD,其中正确结论是_________.(把正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
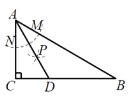
【题目】如图,在Rt△ABC 中,∠C=90°,∠B=30°,以点 A 为圆心,任意长为半径画弧分别交 AB,AC 于点M 和 N,再分别以 M,N 为圆心,大于![]() 的长为半径画弧,两弧交于点 P,连接 AP 并延长交 BC 于点D,则下列说法中:①AD 是∠BAC 的平分线;②点 D 在线段 AB 的垂直平分线上;③S△DAC:S△ABC=1:2.正确的是( ).
的长为半径画弧,两弧交于点 P,连接 AP 并延长交 BC 于点D,则下列说法中:①AD 是∠BAC 的平分线;②点 D 在线段 AB 的垂直平分线上;③S△DAC:S△ABC=1:2.正确的是( ).
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
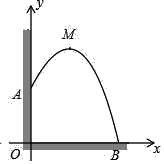
【题目】从某幢建筑物10m高的窗口A处用水管向外喷水,喷出的水成抛物线状(抛物线所在平面与地面垂直).抛物线的最高点M离墙1m,离地面![]() m.
m.
(1)建立适当的平面直角坐标系,求抛物线的解析式.
(2)求水的落地点B与点O的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )

A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BDA=∠CDA
查看答案和解析>>
科目:初中数学 来源: 题型:
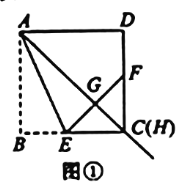
【题目】在正方形![]() 中,过点A引射线
中,过点A引射线![]() ,交边
,交边![]() 于点H(H不与点D重合).通过翻折,使点B落在射线
于点H(H不与点D重合).通过翻折,使点B落在射线![]() 上的点G处,折痕
上的点G处,折痕![]() 交
交![]() 于E,连接E,G并延长
于E,连接E,G并延长![]() 交
交![]() 于F.
于F.
(1)如图1,当点H与点C重合时,![]() 与
与![]() 的大小关系是_________;
的大小关系是_________;![]() 是____________三角形.
是____________三角形.
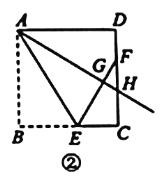
(2)如图2,当点H为边![]() 上任意一点时(点H与点C不重合).连接
上任意一点时(点H与点C不重合).连接![]() ,猜想
,猜想![]() 与
与![]() 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
(3)在图2,当![]() ,
,![]() 时,求
时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
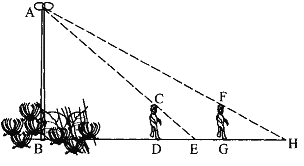
【题目】如图,花丛中有一路灯杆AB. 在灯光下,小明在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时小明的影长GH=5米. 如果小明的身高为1.7米,求路灯杆AB的高度(精确到0.1米).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com