
| A. | 对P有无限多个位置,使得S<2CP2 | |
| B. | 对P有有限多个位置,使得S<2CP2 | |
| C. | 当且仅当P为AB的中点,或者P与顶点A,B之一有重合时,才有S=2CP2 | |
| D. | 对直线AB上的所有点P,总有S=2CP2 |
分析 此题分两种情况讨论:①当P在线段AB上,②当P在直线AB上(线段AB以外的部分);可利用勾股定理来探讨符合要求的点P有哪些.
解答 解:当P为AB上时,假设P为中点时,AP=PB=PC,满足条件,
当点P不为中点时,过点C作AB的垂线,亦满足条件;
当点P在BA的延长线上时,过点P作PF⊥BC,PE⊥CA;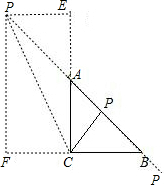
PC2=PF2+CF2,AP2=AE2+PE2=AE2+FC2=2CF2
PB2=BF2+PF2=PF2+(BC+CF)2=2PF2
AP2+PB2=2CF2+PF2+PF2
2PC2=2PF2+2CF2
所以AP2+PB2=2PC2,
即k=2CP2;
同理,当点P在AB的延长线上时,S=2CP2.
综上可知:S=2CP2.
故选D.
点评 此题主要考查的是等腰直角三角形的性质,勾股定理的应用,解法并不复杂,难点在于将问题考虑全面.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | B、C两点到AE的距离相等 | B. | 点E到AB、AC的距离相等 | ||
| C. | B、C两点到点D的距离相等 | D. | B、C两点到AD的距离相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1<a<2 | B. | -2<a<0 | C. | -3≤a≤-3 | D. | -10<a<-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 | ||||
| E. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 当x是有理数时,x2≥0 | |
| B. | 某电影院今天的上座率超过80% | |
| C. | 射击运动员射击一次,命中8环 | |
| D. | 掷一枚普通的正方体骰子出现点数为6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com