
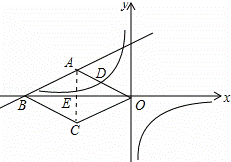
如图,在平面直角坐标系中,四边形ABCD是菱形,B、O在x轴负半轴上,AO=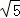 ,tan∠AOB=
,tan∠AOB=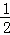 ,一次函数y=k1x+b的图象过A、B两点,反比例函数y=
,一次函数y=k1x+b的图象过A、B两点,反比例函数y=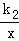 的图象过OA的中点D.
的图象过OA的中点D.
(1)求一次函数和反比例函数的表达式;
(2)平移一次函数y=k1x+b的图象,当一次函数y=k1x+b的图象与反比例函数y=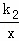 的图象无交点时,求b的取值范围.
的图象无交点时,求b的取值范围.

解:(1)连接AC,交OB于E,如图所示:
∵四边形ABCO是菱形,
∴BE=OE=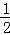 OB,OB⊥AC,
OB,OB⊥AC,
∴∠AEO=90°,
∴tan∠AOB=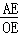 =
=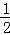 ,
,
∴OE=2AE,
设AE=x,则OE=2x,
根据勾股定理得:OA=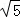 x=
x=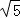 ,
,
∴x=1,
∴AE=1,OE=2,
∴OB=2OE=4,
∴A(﹣2,1),B(﹣4,0),
把点A(﹣2,1),B(﹣4,0)代入一次函数y=k1x+b得: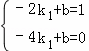 ,
,
解得:k1=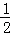 ,b=2,
,b=2,
∴一次函数的解析式为:y=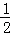 x+2;
x+2;
∵D是OA的中点,A(﹣2,1),
∴D(﹣1,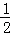 ),
),
把点D(﹣1,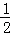 )代入反比例函数y=
)代入反比例函数y=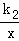 得:k2=﹣
得:k2=﹣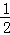 ,
,
∴反比例函数的解析式为:y=﹣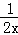 ;
;
(2)根据题意得:一次函数的解析式为:y=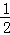 x+b,
x+b,
∵一次函数y=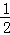 x+b的图象与反比例函数y=﹣
x+b的图象与反比例函数y=﹣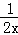 的图象无交点,
的图象无交点,
∴方程组 无解,
无解,
即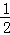 x+b=﹣
x+b=﹣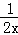 无解,
无解,
整理得:x2+2bx+1=0,
∴△=(2b)2﹣4×1×1<0,b2<1,
解得:﹣1<b<1,
∴当一次函数y=k1x+b的图象与反比例函数y=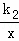 的图象无交点时,b的取值范围是﹣1<b<1.
的图象无交点时,b的取值范围是﹣1<b<1.


科目:初中数学 来源:2014-2015学年江苏省无锡市九年级上学期期中考试数学试卷(解析版) 题型:解答题
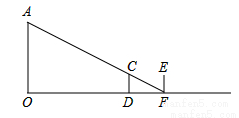
(本题满分5分)如图,小亮晚上在路灯下散步,已知灯杆OA=6.4m,他从灯杆底部的点O处沿直线前进9m到点D时,其影长DF=3m,当他继续前进到达点F时,其影子是变长还是变短?变化量为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
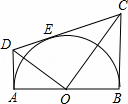
如图,AB为半圆O的在直径,AD、BC分别切⊙O于A、B两点,CD切⊙O于 点E,连接OD、OC,下列结论:①∠DOC=90°,②AD+BC=CD,③S△AOD:S△BOC=AD2:AO2,④OD:OC=DE:EC,⑤OD2=DE•CD,正确的有( )
点E,连接OD、OC,下列结论:①∠DOC=90°,②AD+BC=CD,③S△AOD:S△BOC=AD2:AO2,④OD:OC=DE:EC,⑤OD2=DE•CD,正确的有( )
|
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
2014年中国吸引外国投资达1280亿美元,成为全球外国投资第一大目的地国,将1280亿美元用科学记数法表示为( )
A. 12.8×1010美元 B. 1.28×1011美元
C. 1.28×1012美元 D. 0.128×1013美元
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC中,AB=5,AC=3,BC=4,将△ABC绕点A逆时针旋转30°后得到△ADE,点B经过的路径为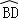 ,则图中阴影部分的面积为( )
,则图中阴影部分的面积为( )
A. 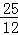 π B.
π B. 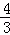 π C.
π C. 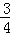 π D.
π D. 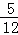 π
π
查看答案和解析>>
科目:初中数学 来源: 题型:
已知抛物线y=x2+bx+c经过A(﹣1,0),B(3,0)两点,与y轴相交于点C,该抛物线的顶点为点D.
(1)求该抛物线的解析式及点D的坐标;
(2)连接AC,CD,BD,BC,设△AOC,△BOC,△BCD的面积分别为S1,S2和S3,用等式表示S1,S2,S3之间的数量关系,并说明理由;
(3)点M是线段AB上一动点(不包括点A和点B),过点M作MN∥BC交AC于点N,连接MC,是否存在点M使∠AMN=∠ACM?若存在,求出点M的坐标和此时刻直线MN的解析式;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com