
【题目】为了方便居民低碳出行,聊城市公共自行车租赁系统(一期)试运行.图①是公共自行车的实物图,图②是公共自行车的车架示意图,点A、D、C、E在同一条直线上,CD=30cm,DF=20cm,AF=25cm,FD⊥AE于点D,座杆CE=15cm,且∠EAB=75°. 
(1)求AD的长;
(2)求点E到AB的距离.(精确到0.1cm,参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)
科目:初中数学 来源: 题型:
【题目】完成推理过程
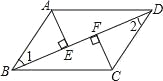
如图,AB∥DC,AE⊥BD,CF⊥BD,BF=DE.求证:AE=CF.
证明∵AB∥DC,
∴∠1= .
∵AE⊥BD,CF⊥BD,
∴∠AEB=
∵BF=DE,
∴BF﹣EF=DE﹣EF
∴ = .
∴△ABE≌△CDF .
∴AE=CF
查看答案和解析>>
科目:初中数学 来源: 题型:
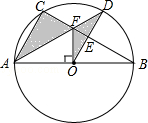
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,FO⊥AB,垂足为点O,连接AF并延长交⊙O于点D,连接OD交BC于点E,∠B=30°,FO=2 ![]() .
. 
(1)求AC的长度;
(2)求图中阴影部分的面积.(计算结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张骑自行车匀速从甲地到乙地,在途中因故停留了一段时间后,仍按原速骑行,小李骑摩托车比小张晚出发一段时间,以800米/分的速度匀速从乙地到甲地,两人距离乙地的路程y(米)与小张出发后的时间x(分)之间的函数图象如图所示.
(1)求小张骑自行车的速度;
(2)求小张停留后再出发时y与x之间的函数表达式;
(3)求小张与小李相遇时x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣ ![]() +bx+c图象经过A(﹣1,0),B(4,0)两点.
+bx+c图象经过A(﹣1,0),B(4,0)两点.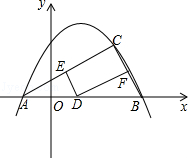
(1)求抛物线的解析式;
(2)若C(m,m﹣1)是抛物线上位于第一象限内的点,D是线段AB上的一个动点(不与A、B重合),过点D分别作DE∥BC交AC于E,DF∥AC交BC于F.
①求证:四边形DECF是矩形;
②试探究:在点D运动过程中,DE、DF、CF的长度之和是否发生变化?若不变,求出它的值,若变化,试说明变化情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知某船于上午8时在A处观测小岛C在北偏东60°方向上,该船以每小时20海里的速度向东航行到B处,测得小岛C在北偏东30°方向上,船以原来的速度继续向东航行2小时,到达岛C正南方点D处,船从A到D一共航行了多少海里?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为Rt△ABC斜边AB上一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD. 
(1)求证:AD平分∠BAC;
(2)若∠BAC=60°,OA=2,求阴影部分的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
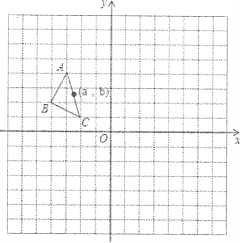
【题目】如图,在平面直角坐标系中,AABC的三个顶点坐标为A(一3,4),B(一4,2),C(一2,1),ΔABC绕原点顺时针旋转90°,得到△A1B1C1,ΔA1B1C1向左平移2个单位,再向下平移5个单位得到△A2B2C2.
(1)画出ΔA1B1Cl和△A2B2C2
(2)P(a,b)是AABC的AC边上一点,ΔABC经旋转、平移后点P的对应点分别为P1、P2,请写出点P1、P2的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com