
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,FO⊥AB,垂足为点O,连接AF并延长交⊙O于点D,连接OD交BC于点E,∠B=30°,FO=2 ![]() .
. 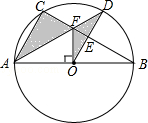
(1)求AC的长度;
(2)求图中阴影部分的面积.(计算结果保留根号)
【答案】
(1)解:∵OF⊥AB,
∴∠BOF=90°,
∵∠B=30°,FO=2 ![]() ,
,
∴OB=6,AB=2OB=12,
又∵AB为⊙O的直径,
∴∠ACB=90°,
∴AC= ![]() AB=6
AB=6
(2)解:∵由(1)可知,AB=12,
∴AO=6,即AC=AO,
在Rt△ACF和Rt△AOF中,
![]()
∴Rt△ACF≌Rt△AOF,
∴∠FAO=∠FAC=30°,
∴∠DOB=60°,
过点D作DG⊥AB于点G,
∵OD=6,∴DG=3 ![]() ,
,
∴S△ACF+S△OFD=S△AOD= ![]() ×6×3
×6×3 ![]() =9
=9 ![]() ,
,
即阴影部分的面积是9 ![]()
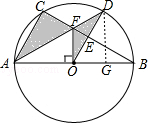
【解析】(1)解直角三角形求出OB,求出AB,根据圆周角定理求出∠ACB,解直角三角求出AC即可;(2)求出△ACF和△AOF全等,得出阴影部分的面积=△AOD的面积,求出三角形的面积即可.


科目:初中数学 来源: 题型:
【题目】今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用的时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示,下列说法错误的是( )

A.小明中途休息用了20分钟
B.小明休息前爬山的平均速度为每分钟70米
C.小明在上述过程中所走的路程为6600米
D.小明休息前爬山的平均速度大于休息后爬山的平均速度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,分别以AB、AC为边作△ABD和△ACE,且AD=AB,AC=AE,∠DAB=∠CAE,连接DC与BE.G、F分别是DC与BE的中点.
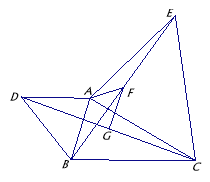
(1)求证:DC=BE;
(2)当∠DAB=80°,求∠AFG的度数;
(3)若∠DAB=![]() ,则∠AFG与
,则∠AFG与![]() 的数量关系是 .
的数量关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)画出△A1B1C1沿x轴向右平移4个单位长度后得到的△A2B2C2;
(3)如果AC上有一点M(a,b)经过上述两次变换,那么对应A2C2上的点M2的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求一个正数的算术平方根,有些数可以直接求得,如![]() ,有些数则不能直接求得,如
,有些数则不能直接求得,如![]() ,但可以通过计算器求. 还有一种方法可以通过一组数的内在联系,运用规律求得,请同学们观察下表:
,但可以通过计算器求. 还有一种方法可以通过一组数的内在联系,运用规律求得,请同学们观察下表:
n | 16 | 0.16 | 0.0016 | 1600 | 160000 | … |
| 4 | 0.4 | 0.04 | 40 | 400 | … |
(1)若![]() ,则
,则![]()
(2)根据你发现的规律,探究下列问题:已知![]() ≈1.435,则:
≈1.435,则:
①![]() ≈ ;
≈ ;
②![]() ≈ ;
≈ ;
(3)根据上述探究过程类比研究一个数的立方根已知![]() ≈1.260,则
≈1.260,则![]() ≈ .
≈ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了增强学生体质,全面实施“学生饮用奶”营养工程.某品牌牛奶供应商提供了原味、草莓味、菠萝味、香橙味、核桃味五种口味的牛奶提供学生饮用.浠马中学为了了解学生对不同口味牛奶的喜好,对全校订购牛奶的学生进行了随机调查(每盒各种口味牛奶的体积相同),绘制了如图两张不完整的人数统计图: 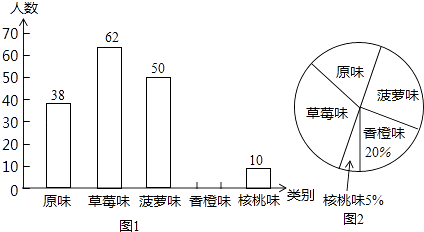
(1)本次被调查的学生有名;
(2)补全上面的条形统计图1,并计算出喜好“菠萝味”牛奶的学生人数在扇形统计图中所占圆心角的度数;
(3)该校共有1200名学生订购了该品牌的牛奶,牛奶供应商每天只为每名订购牛奶的学生配送一盒牛奶.要使学生每天都喝到自己喜好的口味的牛奶,牛奶供应商每天送往该校的牛奶中,草莓味要比原味多送多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)求出△ABC的面积;
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(3)写出点A1,B1,C1的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了方便居民低碳出行,聊城市公共自行车租赁系统(一期)试运行.图①是公共自行车的实物图,图②是公共自行车的车架示意图,点A、D、C、E在同一条直线上,CD=30cm,DF=20cm,AF=25cm,FD⊥AE于点D,座杆CE=15cm,且∠EAB=75°. 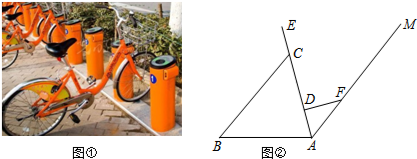
(1)求AD的长;
(2)求点E到AB的距离.(精确到0.1cm,参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠ABC、∠ACB 的角平分线交于点 O,MN 过点 O,且MN∥BC,分别交 AB、AC 于点 M、N.若 MN=5cm,CN=2cm,则 BM=________cm.
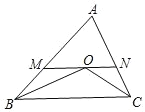
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com