
【题目】为了贯彻落实《关于开展全市义务教育学生体质抽测工作的通知》精神,推进青少年茁壮成长工程,我市决定继续开展市直初中生体质抽测工作。我校初三某班被抽中,已知各人选测项目为下列选项中的任意一项:引体向上(男生)、仰卧起坐(女生)、立定跳远(男、女生),坐位体前屈(男、女生)。
(1)男生小磊抽测引体向上的概率是 ;
(2)用树状图或列表法求男生小磊与女生小铭恰好都抽测坐位体前屈的概率.
科目:初中数学 来源: 题型:
【题目】已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.
(1)求证:AB=AF;
(2)若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
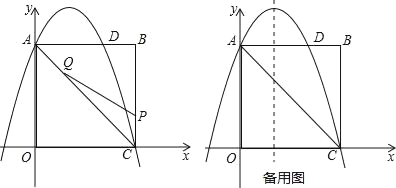
【题目】如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=﹣![]() x2+bx+c经过点A、C,与AB交于点D.
x2+bx+c经过点A、C,与AB交于点D.
(1)求抛物线的函数解析式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式;
②当S最大时,在抛物线y=﹣![]() x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,反比例函数y= ![]() 的图象与一次函数y=x+b的图象交
的图象与一次函数y=x+b的图象交
于点A(1,4)、点B(-4,n).

(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
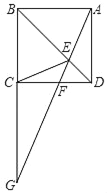
【题目】如图,四边形ABCD是矩形,E是BD上的一点,∠BAE=∠BCE,∠AED=∠CED,点G是BC,AE延长线的交点,AG与CD相交于点F.
(1)求证:四边形ABCD是正方形;
(2)当AE=3EF,DF=1时,求GF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
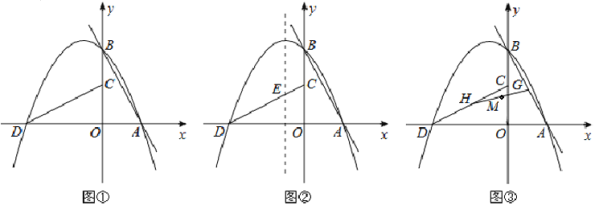
【题目】如图①,定义:直线![]() (m<0, n>0) 与x、y轴分别相交于A、B两点,将△AOB绕着点O逆时针旋转90°得到△COD,过点A、B、D的抛物线P叫做直线l的“纠缠抛物线”,反之,直线l叫做P的“纠缠直线”,两线“互为纠缠线”。
(m<0, n>0) 与x、y轴分别相交于A、B两点,将△AOB绕着点O逆时针旋转90°得到△COD,过点A、B、D的抛物线P叫做直线l的“纠缠抛物线”,反之,直线l叫做P的“纠缠直线”,两线“互为纠缠线”。
(1) 若![]() ,则纠缠抛物线P的函数解析式是 .
,则纠缠抛物线P的函数解析式是 .
(2) 判断并说明![]() 与
与![]() 是否“互为纠缠线”.
是否“互为纠缠线”.
(3) 如图②,若纠缠直线![]() ,纠缠抛物线P的对称轴与CD相交于点E,点F在l上,点Q在P的对称轴上,当以点C、E、Q、F为顶点的四边形是以CE为一边的平行四边形时,求点Q的坐标.
,纠缠抛物线P的对称轴与CD相交于点E,点F在l上,点Q在P的对称轴上,当以点C、E、Q、F为顶点的四边形是以CE为一边的平行四边形时,求点Q的坐标.
(4) 如图③,在(3)的条件下,G为线段AB上的一个动点,G点随着△AOB旋转到线段CD上的H点,连接H、G,取HG的中点M,当点G从A开始运动到B点,直接写出点M的运动路径长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点.
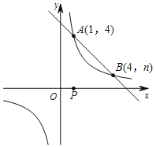
(1)求反比例函数和一次函数的解析式;
(2)直接写出当x>0时,![]() 的解集.
的解集.
(3)点P是x轴上的一动点,试确定点P并求出它的坐标,使PA+PB最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
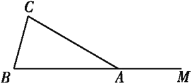
【题目】如图,在△ABC中,AB=AC,点M在BA的延长线上.
(1)按下列要求作图,并在图中标明相应的字母.(保留作图痕迹)
①作∠MAC的平分线AN;
②作AC的中点O,连结BO,并延长BO交AN于点D,连结CD;
(2)在(1)的条件下,判断四边形ABCD的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以Rt△ABC的直角边AB为直径作⊙O与斜边AC交于点D,E为BC边的中点,连接DE、OE.
(1)求证:DE是⊙O的切线;
(2)填空:
①当∠CAB= 时,四边形AOED是平行四边形;
②连接OD,在①的条件下探索四边形OBED的形状为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com