
【题目】如图,在△ABC中,AB=AC,点M在BA的延长线上.
(1)按下列要求作图,并在图中标明相应的字母.(保留作图痕迹)
①作∠MAC的平分线AN;
②作AC的中点O,连结BO,并延长BO交AN于点D,连结CD;
(2)在(1)的条件下,判断四边形ABCD的形状,并证明你的结论.
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)作一个角的平分线和线段的垂直平分线可完成作图;
(2)由AB=AC得∠ACB=∠ABC,由AN平分∠MAC得到∠MAN=∠CAN,则利用三角形外角的性质可得到∠ACB=∠CAD,所以BC∥AD,于是可证明△BOC≌△DOA,得到BC=AD,然后根据平行四边形的判定方法可判断四边形ABCD是平形四边形.
(1)作∠MAC的角平分线AN,作AC的中垂线得到AC的中点O,连接BO,并延长BO交AN于点D,连接CD,如图;
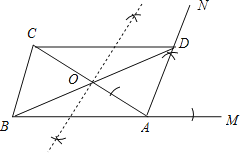
(2)四边形ABCD是平形四边形,理由如下:
∵AB=AC
∴∠ACB=∠ABC,
∵AN平分∠MAC,
∴∠MAN=∠CAN,
∵∠MAC=∠ABC+∠ACB,
∴∠ACB=∠CAD,
∴BC∥AD,
∵AC的中点是O
∴AO=CO,
在△BOC和△DOA中
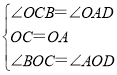
∴△BOC≌△DOA,
∴BC=AD,
而BC∥AD,
∴四边形ABCD是平形四边形.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】某校在争创“全国文明城市”活动中,组织全体学生参加了“创文”知识竞赛,为了解各年级成绩情况,学校这样做的:
(收集数据)从七、八、九三个年级的竞赛成绩中各随机抽取了10名学生成绩如下表:
七年级 | 60 | 70 | 60 | 100 | 80 | 70 | 80 | 60 | 40 | 90 |
八年级 | 80 | 80 | 100 | 40 | 70 | 60 | 80 | 90 | 50 | 80 |
九年级 | 70 | 50 | 60 | 90 | 100 | 80 | 80 | 90 | 70 | 70 |
(整理、描述数据)(说明:80≤x≤100为优秀,60≤x<80为合格,40≤x<60为一般)
年级 | 40≤x<60 | 60≤x<80 | 80≤x≤100 |
七年级 | 1 | 5 | 4 |
八年级 | 2 | 2 | 6 |
九年级 | 1 | 4 | 5 |
年级 | 平均数 | 众数 | 中位数 |
七年级 | a | 60 | 70 |
八年级 | 73 | b | 80 |
九年级 | 76 | 70 | c |
(分析数据)三组样本数据的平均分、众数、中位数如上表所示,其中a= ,b= ,c= .
(得出结论)请你根据以上信息,推断你认为成绩好的年级,并说明理由(至少从两个角度说明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了贯彻落实《关于开展全市义务教育学生体质抽测工作的通知》精神,推进青少年茁壮成长工程,我市决定继续开展市直初中生体质抽测工作。我校初三某班被抽中,已知各人选测项目为下列选项中的任意一项:引体向上(男生)、仰卧起坐(女生)、立定跳远(男、女生),坐位体前屈(男、女生)。
(1)男生小磊抽测引体向上的概率是 ;
(2)用树状图或列表法求男生小磊与女生小铭恰好都抽测坐位体前屈的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
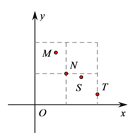
【题目】“单词的记忆效率”是指复习一定量的单词,一周后能正确默写出的单词个数与复习的单词个数的比值.右图描述了某次单词复习中![]() 四位同学的单词记忆效率
四位同学的单词记忆效率![]() 与复习的单词个数
与复习的单词个数![]() 的情况,则这四位同学在这次单词复习中正确默写出的单词个数最多的是( )
的情况,则这四位同学在这次单词复习中正确默写出的单词个数最多的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分10分)
如图,在□ABCD中,以点A为圆心,AB长为半径画弧交AD于点F;再分别以点B、F为圆心,大于![]() BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
(1)根据以上尺规作图的过程,求证四边形ABEF是菱形;
(2)若菱形ABEF的周长为16,AE=4![]() ,求∠C的大小.
,求∠C的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
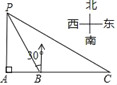
【题目】如图,某海监船以20海里/小时的速度在某海域执行巡航任务,当海监船由西向东航行至A处时,测得岛屿P恰好在其正北方向,继续向东航行1小时到达B处,测得岛屿P在其北偏西30°方向,保持航向不变又航行2小时到达C处,此时海监船与岛屿P之间的距离(即PC的长)为( )
A. 40海里 B. 60海里 C. 20![]() 海里 D. 40
海里 D. 40![]() 海里
海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC的中点,∠BAD=![]() ∠BAC=60°,于是
∠BAC=60°,于是![]() ;
;
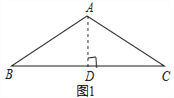
迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=120°,D,E,C三点在同一条直线上,连接BD.
(1)求证:△ADB≌△AEC;
(2)若AD=2,BD=3,请计算线段CD的长;
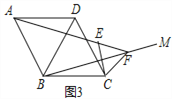
拓展延伸:如图3,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE,CF.
(3)证明:△CEF是等边三角形;
(4)若AE=4,CE=1,求BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
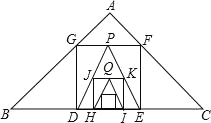
【题目】如图,已知在Rt△ABC中,AB=AC=3![]() ,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,则第2014个内接正方形的边长为____.
,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,则第2014个内接正方形的边长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 分别与x轴,y轴交于点
分别与x轴,y轴交于点![]() ,点C是第一象限内的一点,且
,点C是第一象限内的一点,且![]() ,抛物线
,抛物线![]() 经过
经过![]() 两点,与x轴的另一交点为D.
两点,与x轴的另一交点为D.
(1)求此抛物线的解析式;
(2)判断直线![]() 与
与![]() 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以![]() 四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com