
【题目】某校在争创“全国文明城市”活动中,组织全体学生参加了“创文”知识竞赛,为了解各年级成绩情况,学校这样做的:
(收集数据)从七、八、九三个年级的竞赛成绩中各随机抽取了10名学生成绩如下表:
七年级 | 60 | 70 | 60 | 100 | 80 | 70 | 80 | 60 | 40 | 90 |
八年级 | 80 | 80 | 100 | 40 | 70 | 60 | 80 | 90 | 50 | 80 |
九年级 | 70 | 50 | 60 | 90 | 100 | 80 | 80 | 90 | 70 | 70 |
(整理、描述数据)(说明:80≤x≤100为优秀,60≤x<80为合格,40≤x<60为一般)
年级 | 40≤x<60 | 60≤x<80 | 80≤x≤100 |
七年级 | 1 | 5 | 4 |
八年级 | 2 | 2 | 6 |
九年级 | 1 | 4 | 5 |
年级 | 平均数 | 众数 | 中位数 |
七年级 | a | 60 | 70 |
八年级 | 73 | b | 80 |
九年级 | 76 | 70 | c |
(分析数据)三组样本数据的平均分、众数、中位数如上表所示,其中a= ,b= ,c= .
(得出结论)请你根据以上信息,推断你认为成绩好的年级,并说明理由(至少从两个角度说明)
科目:初中数学 来源: 题型:
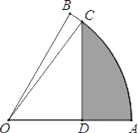
【题目】如图,扇形OAB中,∠AOB=60°,扇形半径为4,点C在![]() 上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为_____.
上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.
(1)求证:AB=AF;
(2)若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
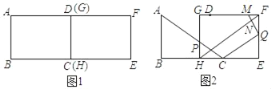
【题目】把两个全等的矩形ABCD和EFGH如图1摆放(点D和点G重合,点C和点H重合),点A、D(G)在同一条直线上,AB=6cm,BC=8cm.如图2,△ABC从图1位置出发,沿BC方向匀速运动,速度为1cm/s,AC与GH交于点P;同时,点Q从点E出发,沿EF方向匀速运动,速度为1cm/s.点Q停止运动时,△ABC也停止运动.设运动时间为t(s)(0<t<6).
(1)当t为何值时,CQ∥FH;
(2)过点Q作QM⊥FH于点N,交GF于点M,设五边形GBCQM的面积为y(cm2),求y与t之间的函数关系式;
(3)在(2)的条件下,是否存在某一时刻,使点M在线段PC的中垂线上?若存在,请求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
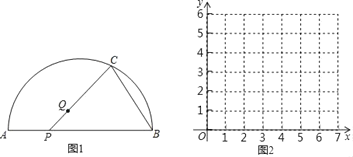
【题目】如图,点P是![]() 所对弦AB上一动点,点Q是
所对弦AB上一动点,点Q是![]() 与弦AB所围成的图形的内部的一定点,作射线PQ交
与弦AB所围成的图形的内部的一定点,作射线PQ交![]() 于点C,连接BC.已知AB=6cm,设A,P两点间的距离为xcm,P,C两点间的距离为y1cm,B,C两点间的距离为y2cm.(当点P与点A重合时,x的值为0).
于点C,连接BC.已知AB=6cm,设A,P两点间的距离为xcm,P,C两点间的距离为y1cm,B,C两点间的距离为y2cm.(当点P与点A重合时,x的值为0).
小平根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.
下面是小平的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y与x的几组对应值;
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 5.37 | 4.06 | 2.83 | m | 3.86 | 4.83 | 5.82 |
y2/cm | 2.68 | 3.57 | 4.90 | 5.54 | 5.72 | 5.79 | 5.82 |
经测量m的值是(保留一位小数).
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数y1,y2的图象;
(3)结合函数图象,解决问题:当△BCP为等腰三角形时,AP的长度约为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,等腰Rt△ABC中,∠C=90o,D是AB的中点,Rt△DEF的两条直角边DE、DF分别与AC、BC相交于点M、N.
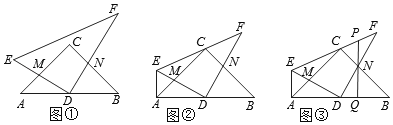
(1)思考推证:CM+CN=BC;
(2)探究证明:如图②,若EF经过点C,AE⊥AB,判断线段MA、ME、MC、DN四条线段之间的数量关系,并证明你的结论;
(3)拓展应用:如图③,在②的条件下,若AB=4,AE=1,Q为线段DB上一点,DQ=![]() ,QN的延长线交EF于点P,求线段PQ的长.
,QN的延长线交EF于点P,求线段PQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
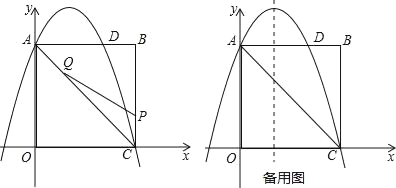
【题目】如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=﹣![]() x2+bx+c经过点A、C,与AB交于点D.
x2+bx+c经过点A、C,与AB交于点D.
(1)求抛物线的函数解析式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式;
②当S最大时,在抛物线y=﹣![]() x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,反比例函数y= ![]() 的图象与一次函数y=x+b的图象交
的图象与一次函数y=x+b的图象交
于点A(1,4)、点B(-4,n).

(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
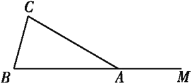
【题目】如图,在△ABC中,AB=AC,点M在BA的延长线上.
(1)按下列要求作图,并在图中标明相应的字母.(保留作图痕迹)
①作∠MAC的平分线AN;
②作AC的中点O,连结BO,并延长BO交AN于点D,连结CD;
(2)在(1)的条件下,判断四边形ABCD的形状,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com