
【题目】如图①,等腰Rt△ABC中,∠C=90o,D是AB的中点,Rt△DEF的两条直角边DE、DF分别与AC、BC相交于点M、N.
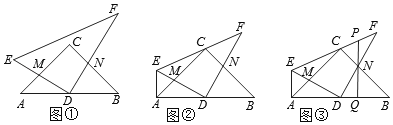
(1)思考推证:CM+CN=BC;
(2)探究证明:如图②,若EF经过点C,AE⊥AB,判断线段MA、ME、MC、DN四条线段之间的数量关系,并证明你的结论;
(3)拓展应用:如图③,在②的条件下,若AB=4,AE=1,Q为线段DB上一点,DQ=![]() ,QN的延长线交EF于点P,求线段PQ的长.
,QN的延长线交EF于点P,求线段PQ的长.
【答案】(1)详见解析;(2)![]() ,证明详见解析;(3)
,证明详见解析;(3)![]() .
.
【解析】
(1)如图1,连接CD.证明△BDN≌△CDM,即可解决问题;
(2)结论:![]() .利用相似三角形的性质即可解答.
.利用相似三角形的性质即可解答.
(3)如图3,连接CD,作EH⊥CD于H,证明△PNC≌△EAM,求出PN、QN的值即可解决问题.
(1)证明:连接CD,
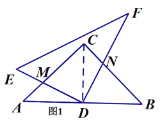

∵∠ACB=90,CA=CB,AD=DB,∴CD=AD=DB=![]() AB,
AB,
∠A=∠B=∠ACD=∠BCD=45,CD⊥AB,
∴∠CDN+∠BDN=90,
∵∠EDF=90,∴∠CDN+CDM=90,∴∠BDN=∠CDM,
∴△BDN≌△CDM, ∴BN=CM,
∴ BC=BN+CN=CM+CN;
(2)∵AE⊥AB,CD⊥AB,∴AE∥CD
∴△AEM∽△CDM,∴![]() ,
,
∵△BDN≌△CDM,∴DN=DM,
∴![]() ,即
,即![]() ;
;
(3)∵∠EDF=90,∴∠NDQ+∠ADE=90
∵EA⊥AD,∴∠AED+∠ADE=90 ,∴∠AED=∠NDQ
而AE=1,AD=CD=DB=![]() AB=2,∴ED=
AB=2,∴ED=![]()
∵△AEM∽△CDM,∴![]() ,∴DM=DN=
,∴DM=DN=![]() ED=
ED=![]() ,
,
而DQ=![]() ,∴
,∴![]() ,
,
∴△AED∽△QDN,![]()
过点E作EH⊥CD于点H,∴DH=AE=1,EH=AD=2,∴CH=2-1=1,

∴EC=![]() ,∴EC=ED,∴∠ECD=∠EDC=∠AEM,
,∴EC=ED,∴∠ECD=∠EDC=∠AEM,
∵PQ⊥AB,∴∠B=∠BNQ=∠PNC=45,
而∠PCN+∠NCD+∠ECD=∠EMA+∠AEM+∠EAM=180,
∠PCN=∠AME,而∠EAM=∠PNC=45,CN=AM,
∴△PNC≌△EAM,∴PN=AE=1,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】某服装公司招工广告承诺:熟练工人每月工资至少3000元.每天工作8小时,一个月工作25天.月工资底薪800元,另加计件工资.加工1件A型服装计酬16元,加工1件B型服装计酬12元.在工作中发现一名熟练工加工1件A型服装和2件B型服装需4小时,加工3件A型服装和1件B型服装需7小时.(工人月工资=底薪+计件工资)
(1)一名熟练工加工1件A型服装和1件B型服装各需要多少小时?
(2)一段时间后,公司规定:“每名工人每月必须加工A,B两种型号的服装,且加工A型服装数量不少于B型服装的一半”.设一名熟练工人每月加工A型服装a件,工资总额为W元.请你运用所学知识判断该公司在执行规定后是否违背了广告承诺?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数![]() 的图象上.若点A的坐标为(﹣4,﹣4),则k的值为( )
的图象上.若点A的坐标为(﹣4,﹣4),则k的值为( )
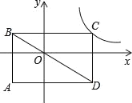
A. 16B. ﹣3C. 5D. 5或﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=kx+b(k<0),经过点(6,0),且与坐标轴围成的三角形的面积是9,与函数y=![]() (x>0)的图象G交于A,B两点.
(x>0)的图象G交于A,B两点.
(1)求直线的表达式;
(2)横、纵坐标都是整数的点叫作整点.记图象G在点A、B之间的部分与线段AB围成的区域(不含边界)为W.
①当m=2时,直接写出区域W内的整点的坐标 ;
②若区域W内恰有3个整数点,结合函数图象,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在争创“全国文明城市”活动中,组织全体学生参加了“创文”知识竞赛,为了解各年级成绩情况,学校这样做的:
(收集数据)从七、八、九三个年级的竞赛成绩中各随机抽取了10名学生成绩如下表:
七年级 | 60 | 70 | 60 | 100 | 80 | 70 | 80 | 60 | 40 | 90 |
八年级 | 80 | 80 | 100 | 40 | 70 | 60 | 80 | 90 | 50 | 80 |
九年级 | 70 | 50 | 60 | 90 | 100 | 80 | 80 | 90 | 70 | 70 |
(整理、描述数据)(说明:80≤x≤100为优秀,60≤x<80为合格,40≤x<60为一般)
年级 | 40≤x<60 | 60≤x<80 | 80≤x≤100 |
七年级 | 1 | 5 | 4 |
八年级 | 2 | 2 | 6 |
九年级 | 1 | 4 | 5 |
年级 | 平均数 | 众数 | 中位数 |
七年级 | a | 60 | 70 |
八年级 | 73 | b | 80 |
九年级 | 76 | 70 | c |
(分析数据)三组样本数据的平均分、众数、中位数如上表所示,其中a= ,b= ,c= .
(得出结论)请你根据以上信息,推断你认为成绩好的年级,并说明理由(至少从两个角度说明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《如果想毁掉一个孩子,就给他一部手机!》这是2017年微信圈一篇热传的文章.国际上,法国教育部宣布从 2018 年9月新学期起小学和初中禁止学生使用手机.为了解学生手机使用情况,某学校开展了“手机伴我健康行”主题活动,他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查,并绘制成如图①,②的 统计图,已知“查资料”的人数是 40人.请你根据以上信息解答下列问题:
(1)在扇形统计图中,“玩游戏”对应的百分比为______,圆心角度数是______度;
(2)补全条形统计图;
(3)该校共有学生2100人,估计每周使用手机时间在2 小时以上(不含2小时)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
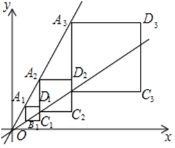
【题目】如图,点A1(1,![]() )在直线y=kx上,过点A1作A1B1∥y轴交直线y=
)在直线y=kx上,过点A1作A1B1∥y轴交直线y=![]() x于点B1,以A1B1为边在A1B1的右侧作正方形A1B1C1D1,直线C1D1分别交直线y=kx和y=
x于点B1,以A1B1为边在A1B1的右侧作正方形A1B1C1D1,直线C1D1分别交直线y=kx和y=![]() x于A2,B2两点,以A2B2为边在A2B2的右侧作等正方形A2B2C2D2…,直线C2D2分别交直线y=kx和y=
x于A2,B2两点,以A2B2为边在A2B2的右侧作等正方形A2B2C2D2…,直线C2D2分别交直线y=kx和y=![]() x于A3,B3两点,以A3B3为边在A3B3的右侧作正方形A3B3C3D3,…,按此规律进行下去,则正方形AnBnCnDn的面积为____________.(用含正整数n的代数式表示)
x于A3,B3两点,以A3B3为边在A3B3的右侧作正方形A3B3C3D3,…,按此规律进行下去,则正方形AnBnCnDn的面积为____________.(用含正整数n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“高低杠”是女子体操特有的一个竞技项目,其比赛器材由高、低两根平行杠及若干支架组成,运动员可根据自己的身高和习惯在规定范围内调节高、低两杠间的距离.某兴趣小组根据高低杠器材的一种截面图编制了如下数学问题,请你解答.
如图所示,底座上A,B两点间的距离为90cm.低杠上点C到直线AB的距离CE的长为155cm,高杠上点D到直线AB的距离DF的长为234cm,已知低杠的支架AC与直线AB的夹角∠CAE为82.4°,高杠的支架BD与直线AB的夹角∠DBF为80.3°.求高、低杠间的水平距离CH的长.(结果精确到1cm,参考数据sin82.4°≈0.991,cos82.4°≈0.132,tan82.4°≈7.500,sin80.3°≈0.983,cos80.3°≈0.168,tan80.3°≈5.850)

查看答案和解析>>
科目:初中数学 来源: 题型:
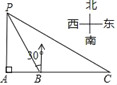
【题目】如图,某海监船以20海里/小时的速度在某海域执行巡航任务,当海监船由西向东航行至A处时,测得岛屿P恰好在其正北方向,继续向东航行1小时到达B处,测得岛屿P在其北偏西30°方向,保持航向不变又航行2小时到达C处,此时海监船与岛屿P之间的距离(即PC的长)为( )
A. 40海里 B. 60海里 C. 20![]() 海里 D. 40
海里 D. 40![]() 海里
海里
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com