
【题目】如图,点A1(1,![]() )在直线y=kx上,过点A1作A1B1∥y轴交直线y=
)在直线y=kx上,过点A1作A1B1∥y轴交直线y=![]() x于点B1,以A1B1为边在A1B1的右侧作正方形A1B1C1D1,直线C1D1分别交直线y=kx和y=
x于点B1,以A1B1为边在A1B1的右侧作正方形A1B1C1D1,直线C1D1分别交直线y=kx和y=![]() x于A2,B2两点,以A2B2为边在A2B2的右侧作等正方形A2B2C2D2…,直线C2D2分别交直线y=kx和y=
x于A2,B2两点,以A2B2为边在A2B2的右侧作等正方形A2B2C2D2…,直线C2D2分别交直线y=kx和y=![]() x于A3,B3两点,以A3B3为边在A3B3的右侧作正方形A3B3C3D3,…,按此规律进行下去,则正方形AnBnCnDn的面积为____________.(用含正整数n的代数式表示)
x于A3,B3两点,以A3B3为边在A3B3的右侧作正方形A3B3C3D3,…,按此规律进行下去,则正方形AnBnCnDn的面积为____________.(用含正整数n的代数式表示)
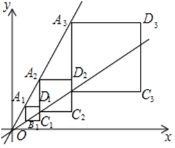
【答案】4n-1
【解析】
先根据点A1的坐标以及A1B1∥y轴,求得B1的坐标,进而得到A1B1的长以及正方形A1B1C1D1的面积,再根据A2的坐标以及A2B2∥y轴,求得B2的坐标,进而得到A2B2的长以及正方形A2B2C2D2的面积,最后根据变换规律,求得AnBn的长,进而得出正方形AnBnCnDn的面积即可.
∵点A1(1,![]() )在直线y=kx上,
)在直线y=kx上,
∴k=![]() ,y=
,y=![]() x.
x.
∵A1B1∥y轴交直线y=![]() x于点B1,
x于点B1,
∴B1(1,![]() ),
),
∴A1B1=![]() -
-![]() =1,即正方形A1B1C1D1的面积=12=1;
=1,即正方形A1B1C1D1的面积=12=1;
∵B1C1=A1B1=1,
∴A2(2,3),
又∵A2B2∥y轴,交直线y=![]() x于点B2,
x于点B2,
∴B2(2,1),
∴A2B2=3-1=2,即正方形A2B2C2D2的面积=22=4;
以此类推,
A3B3=4,即正方形A3B3C3D3的面积=42=16;
A4B4=8,即△A4B4C4面积=82=64=43;
…
∴AnBn=2n-1,即正方形AnBnCnDn的面积=(2n-1)2=4n-1.
故答案为4n-1.


科目:初中数学 来源: 题型:
【题目】如图所示,菱形ABCD位于平面直角坐标系中,抛物线y=ax2+bx+c经过菱形的三个顶点A、B、C,已知A(﹣3,0)、B(0,﹣4).
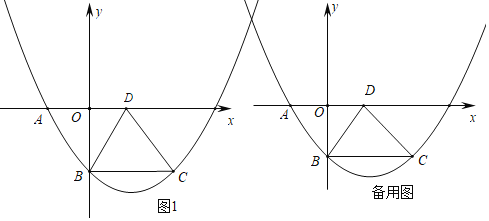
(1)求抛物线解析式;
(2)线段BD上有一动点E,过点E作y轴的平行线,交BC于点F,若S△BOD=4S△EBF,求点E的坐标;
(3)抛物线的对称轴上是否存在点P,使△BPD是以BD为斜边的直角三角形?如果存在,求出点P的坐标;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
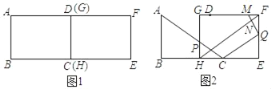
【题目】把两个全等的矩形ABCD和EFGH如图1摆放(点D和点G重合,点C和点H重合),点A、D(G)在同一条直线上,AB=6cm,BC=8cm.如图2,△ABC从图1位置出发,沿BC方向匀速运动,速度为1cm/s,AC与GH交于点P;同时,点Q从点E出发,沿EF方向匀速运动,速度为1cm/s.点Q停止运动时,△ABC也停止运动.设运动时间为t(s)(0<t<6).
(1)当t为何值时,CQ∥FH;
(2)过点Q作QM⊥FH于点N,交GF于点M,设五边形GBCQM的面积为y(cm2),求y与t之间的函数关系式;
(3)在(2)的条件下,是否存在某一时刻,使点M在线段PC的中垂线上?若存在,请求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,等腰Rt△ABC中,∠C=90o,D是AB的中点,Rt△DEF的两条直角边DE、DF分别与AC、BC相交于点M、N.
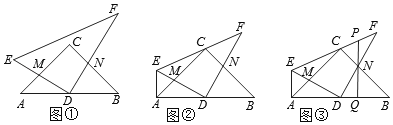
(1)思考推证:CM+CN=BC;
(2)探究证明:如图②,若EF经过点C,AE⊥AB,判断线段MA、ME、MC、DN四条线段之间的数量关系,并证明你的结论;
(3)拓展应用:如图③,在②的条件下,若AB=4,AE=1,Q为线段DB上一点,DQ=![]() ,QN的延长线交EF于点P,求线段PQ的长.
,QN的延长线交EF于点P,求线段PQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
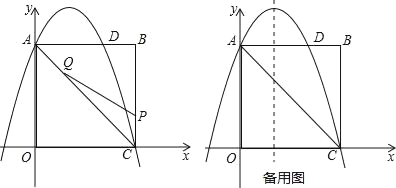
【题目】如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=﹣![]() x2+bx+c经过点A、C,与AB交于点D.
x2+bx+c经过点A、C,与AB交于点D.
(1)求抛物线的函数解析式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式;
②当S最大时,在抛物线y=﹣![]() x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】企业的污水处理有两种方式,一种是输送到污水厂进行集中处理,另一种是通过企业的自身设备进行处理.某企业去年每月的污水量均为12000吨,由于污水厂处于调试阶段,污水处理能力有限,该企业投资自建设备处理污水,两种处理方式同时进行.1至6月,该企业向污水厂输送的污水量y1(吨)与月份x(1≤x≤6,且x取整数)之间满足的函数关系如下表:
月份x(月) | 1 | 2 | 3 | 4 | 5 | 6 |
输送的污水量y1(吨) | 12000 | 6000 | 4000 | 3000 | 2400 | 2000 |
7至12月,该企业自身处理的污水量y2(吨)与月份x(7≤x≤12,且x取整数)之间满足二次函数关系式为![]() (a≠0).其图象如图所示.1至6月,污水厂处理每吨污水的费用:z1(元)与月份x之间满足函数关系式:
(a≠0).其图象如图所示.1至6月,污水厂处理每吨污水的费用:z1(元)与月份x之间满足函数关系式:![]() ,该企业自身处理每吨污水的费用:z2(元)与月份x之间满足函数关系式:
,该企业自身处理每吨污水的费用:z2(元)与月份x之间满足函数关系式:![]() ;7至12月,污水厂处理每吨污水的费用均为2元,该企业自身处理每吨污水的费用均为1.5元.
;7至12月,污水厂处理每吨污水的费用均为2元,该企业自身处理每吨污水的费用均为1.5元.
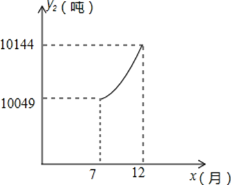
(1)请观察题中的表格和图象,用所学过的一次函数、反比例函数或二次函数的有关知识,分别直接写出y1,y2与x之间的函数关系式;
(2)请你求出该企业去年哪个月用于污水处理的费用W(元)最多,并求出这个最多费用;
(3)今年以来,由于自建污水处理设备的全面运行,该企业决定扩大产能并将所有污水全部自身处理,估计扩大产能后今年每月的污水量都将在去年每月的基础上增加a%,同时每吨污水处理的费用将在去年12月份的基础上增加(a-30)%,为鼓励节能降耗,减轻企业负担,财政对企业处理污水的费用进行50%的补助.若该企业每月的污水处理费用为18000元,请计算出a的整数值.
(参考数据:![]() ≈15.2,
≈15.2,![]() ≈20.5,
≈20.5,![]() ≈28.4)
≈28.4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,反比例函数y= ![]() 的图象与一次函数y=x+b的图象交
的图象与一次函数y=x+b的图象交
于点A(1,4)、点B(-4,n).

(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
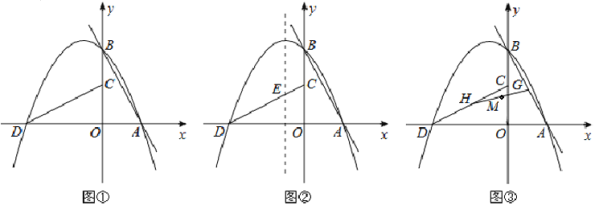
【题目】如图①,定义:直线![]() (m<0, n>0) 与x、y轴分别相交于A、B两点,将△AOB绕着点O逆时针旋转90°得到△COD,过点A、B、D的抛物线P叫做直线l的“纠缠抛物线”,反之,直线l叫做P的“纠缠直线”,两线“互为纠缠线”。
(m<0, n>0) 与x、y轴分别相交于A、B两点,将△AOB绕着点O逆时针旋转90°得到△COD,过点A、B、D的抛物线P叫做直线l的“纠缠抛物线”,反之,直线l叫做P的“纠缠直线”,两线“互为纠缠线”。
(1) 若![]() ,则纠缠抛物线P的函数解析式是 .
,则纠缠抛物线P的函数解析式是 .
(2) 判断并说明![]() 与
与![]() 是否“互为纠缠线”.
是否“互为纠缠线”.
(3) 如图②,若纠缠直线![]() ,纠缠抛物线P的对称轴与CD相交于点E,点F在l上,点Q在P的对称轴上,当以点C、E、Q、F为顶点的四边形是以CE为一边的平行四边形时,求点Q的坐标.
,纠缠抛物线P的对称轴与CD相交于点E,点F在l上,点Q在P的对称轴上,当以点C、E、Q、F为顶点的四边形是以CE为一边的平行四边形时,求点Q的坐标.
(4) 如图③,在(3)的条件下,G为线段AB上的一个动点,G点随着△AOB旋转到线段CD上的H点,连接H、G,取HG的中点M,当点G从A开始运动到B点,直接写出点M的运动路径长。
查看答案和解析>>
科目:初中数学 来源: 题型:
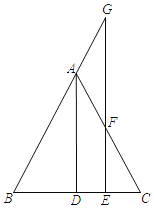
【题目】如图所示,△ABC中,AB=AC,AD平分∠BAC,点G是BA延长线上一点,点F是AC上一点,AG=AF,连接GF并延长交BC于E.
(1)若AB=8,BC=6,求AD的长;
(2)求证:GE⊥BC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com