
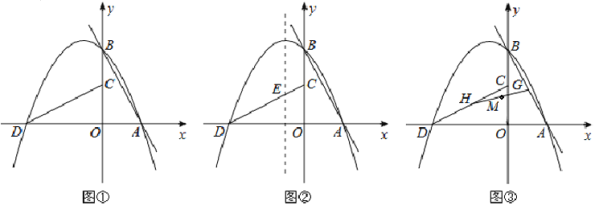
【题目】如图①,定义:直线![]() (m<0, n>0) 与x、y轴分别相交于A、B两点,将△AOB绕着点O逆时针旋转90°得到△COD,过点A、B、D的抛物线P叫做直线l的“纠缠抛物线”,反之,直线l叫做P的“纠缠直线”,两线“互为纠缠线”。
(m<0, n>0) 与x、y轴分别相交于A、B两点,将△AOB绕着点O逆时针旋转90°得到△COD,过点A、B、D的抛物线P叫做直线l的“纠缠抛物线”,反之,直线l叫做P的“纠缠直线”,两线“互为纠缠线”。
(1) 若![]() ,则纠缠抛物线P的函数解析式是 .
,则纠缠抛物线P的函数解析式是 .
(2) 判断并说明![]() 与
与![]() 是否“互为纠缠线”.
是否“互为纠缠线”.
(3) 如图②,若纠缠直线![]() ,纠缠抛物线P的对称轴与CD相交于点E,点F在l上,点Q在P的对称轴上,当以点C、E、Q、F为顶点的四边形是以CE为一边的平行四边形时,求点Q的坐标.
,纠缠抛物线P的对称轴与CD相交于点E,点F在l上,点Q在P的对称轴上,当以点C、E、Q、F为顶点的四边形是以CE为一边的平行四边形时,求点Q的坐标.
(4) 如图③,在(3)的条件下,G为线段AB上的一个动点,G点随着△AOB旋转到线段CD上的H点,连接H、G,取HG的中点M,当点G从A开始运动到B点,直接写出点M的运动路径长。
【答案】解:(1)![]() ;(2)详见解析;(3)Q点坐标为
;(2)详见解析;(3)Q点坐标为![]() 或
或![]() ;(4)M的运动路径长为
;(4)M的运动路径长为![]()
【解析】
(1)根据题意及直线l解析式可得A,B,D坐标,用待定系数法可求抛物线P的函数解析式;
(2)分别在x=0时和y=0时,求两函数与坐标轴交点,然后根据“互为纠缠线”的定义进行判断;
(3)以点C,E,Q,F为顶点的四边形是以CE为一边的平行四边形时,则有FQ∥CE,且FQ=CE.以此为基础,列方程求出点Q的坐标;
(4)如图,过点H,G分别作HJ⊥x轴,GK⊥x轴,由旋转的性质可证明△HJO≌△OKG,则可以设点G(m,-2m+4)(0≤m≤2), H(2m-4,m),得到M点坐标为(![]() ),从而确定出点M在直线
),从而确定出点M在直线![]() (-2≤x≤1)上运动,然后根据两点间距离公式易得结果.
(-2≤x≤1)上运动,然后根据两点间距离公式易得结果.
解:(1)若![]() ,则A(1,0),B(0,2),D(-2,0),
,则A(1,0),B(0,2),D(-2,0),
设抛物线解析式为:y=a(x-1)(x+2),
将B(0,2)代入可得:a=-1,
∴抛物线解析式为:y=-(x-1)(x+2)=![]() ;
;
(2)当x=0时,![]() ,
,![]() ,
,
∴两函数图像交于y轴(0,2k),
当y=0时,①![]() ,解得:x=k,
,解得:x=k,
②![]() ,解得:
,解得:![]() ,
,![]() ,
,
∴两函数图像交于x轴(k,0),且OB=OD,
∴![]() 与
与![]() “互为纠缠线”;
“互为纠缠线”;
(3)若![]() ,则A(2,0),B(0,4),C(0,2),D(-4,0),
,则A(2,0),B(0,4),C(0,2),D(-4,0),
求得直线CD的解析式为:y=![]() ,
,
可求得P的对称轴为![]() .
.
∵以点C,E,Q,F为顶点的四边形是以CE为一边的平行四边形,
∴FQ∥CE,且FQ=CE.
设直线FQ的解析式为:y=![]() ,
,
∵点E、点C的横坐标相差1,
∴点F、点Q的横坐标也是相差1.
则|xF(1)|=|xF+1|=1,
解得xF=0或xF=2.
∵点F在直线l:y=2x+4上,
∴点F坐标为(0,4)或(2,8).
若F(0,4),则直线FQ为:y=![]() +4,
+4,
当x=1时,y=![]() ,
,
∴Q1(1,![]() );
);
若F(2,8),则直线FQ为:y=![]() x+9,
x+9,
当x=1时,y=![]() ,
,
∴Q2(1,![]() ).
).
∴满足条件的点Q有2个,点Q坐标为Q1(1,![]() ), Q2(1,
), Q2(1,![]() ).
).
(4)如图,过点H,G分别作HJ⊥x轴,GK⊥x轴,
∵OH=OG,∠HOG=90°,
∴∠HOJ+∠GOK=90°,
∵∠HOJ+∠JHO=90°,
∴∠GOK=∠JHO,
又∵∠HJO=∠OKG=90°,
∴△HJO≌△OKG,
设点G(m,-2m+4)(0≤m≤2),则H(2m-4,m)
∴M(![]() ),
),
令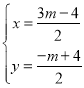 ,
,
∴ ,
,
∴![]() ,
,
∵0≤m≤2,
∴-2≤x≤1,
∴点M在直线![]() (-2≤x≤1)上运动,
(-2≤x≤1)上运动,
当x=1时,y=![]() ,
,
当x=-2时,y=![]() ,
,
∴M的运动路径长=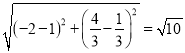



科目:初中数学 来源: 题型:
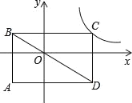
【题目】如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数![]() 的图象上.若点A的坐标为(﹣4,﹣4),则k的值为( )
的图象上.若点A的坐标为(﹣4,﹣4),则k的值为( )
A. 16B. ﹣3C. 5D. 5或﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
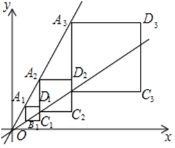
【题目】如图,点A1(1,![]() )在直线y=kx上,过点A1作A1B1∥y轴交直线y=
)在直线y=kx上,过点A1作A1B1∥y轴交直线y=![]() x于点B1,以A1B1为边在A1B1的右侧作正方形A1B1C1D1,直线C1D1分别交直线y=kx和y=
x于点B1,以A1B1为边在A1B1的右侧作正方形A1B1C1D1,直线C1D1分别交直线y=kx和y=![]() x于A2,B2两点,以A2B2为边在A2B2的右侧作等正方形A2B2C2D2…,直线C2D2分别交直线y=kx和y=
x于A2,B2两点,以A2B2为边在A2B2的右侧作等正方形A2B2C2D2…,直线C2D2分别交直线y=kx和y=![]() x于A3,B3两点,以A3B3为边在A3B3的右侧作正方形A3B3C3D3,…,按此规律进行下去,则正方形AnBnCnDn的面积为____________.(用含正整数n的代数式表示)
x于A3,B3两点,以A3B3为边在A3B3的右侧作正方形A3B3C3D3,…,按此规律进行下去,则正方形AnBnCnDn的面积为____________.(用含正整数n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“高低杠”是女子体操特有的一个竞技项目,其比赛器材由高、低两根平行杠及若干支架组成,运动员可根据自己的身高和习惯在规定范围内调节高、低两杠间的距离.某兴趣小组根据高低杠器材的一种截面图编制了如下数学问题,请你解答.
如图所示,底座上A,B两点间的距离为90cm.低杠上点C到直线AB的距离CE的长为155cm,高杠上点D到直线AB的距离DF的长为234cm,已知低杠的支架AC与直线AB的夹角∠CAE为82.4°,高杠的支架BD与直线AB的夹角∠DBF为80.3°.求高、低杠间的水平距离CH的长.(结果精确到1cm,参考数据sin82.4°≈0.991,cos82.4°≈0.132,tan82.4°≈7.500,sin80.3°≈0.983,cos80.3°≈0.168,tan80.3°≈5.850)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了贯彻落实《关于开展全市义务教育学生体质抽测工作的通知》精神,推进青少年茁壮成长工程,我市决定继续开展市直初中生体质抽测工作。我校初三某班被抽中,已知各人选测项目为下列选项中的任意一项:引体向上(男生)、仰卧起坐(女生)、立定跳远(男、女生),坐位体前屈(男、女生)。
(1)男生小磊抽测引体向上的概率是 ;
(2)用树状图或列表法求男生小磊与女生小铭恰好都抽测坐位体前屈的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
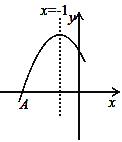
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出以下结论:①abc<0 ②b2﹣4ac>0 ③4b+c<0 ④若B(﹣![]() ,y1)、C(﹣
,y1)、C(﹣![]() ,y2)为函数图象上的两点,则y1>y2⑤当﹣3≤x≤1时,y≥0,
,y2)为函数图象上的两点,则y1>y2⑤当﹣3≤x≤1时,y≥0,
其中正确的结论是(填写代表正确结论的序号)__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
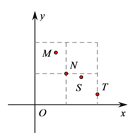
【题目】“单词的记忆效率”是指复习一定量的单词,一周后能正确默写出的单词个数与复习的单词个数的比值.右图描述了某次单词复习中![]() 四位同学的单词记忆效率
四位同学的单词记忆效率![]() 与复习的单词个数
与复习的单词个数![]() 的情况,则这四位同学在这次单词复习中正确默写出的单词个数最多的是( )
的情况,则这四位同学在这次单词复习中正确默写出的单词个数最多的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
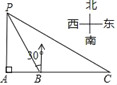
【题目】如图,某海监船以20海里/小时的速度在某海域执行巡航任务,当海监船由西向东航行至A处时,测得岛屿P恰好在其正北方向,继续向东航行1小时到达B处,测得岛屿P在其北偏西30°方向,保持航向不变又航行2小时到达C处,此时海监船与岛屿P之间的距离(即PC的长)为( )
A. 40海里 B. 60海里 C. 20![]() 海里 D. 40
海里 D. 40![]() 海里
海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0),过(1,y1)、(2,y2).下列结论:①若y1>0时,则a+b+c>0; ②若a=2b时,则y1<y2;③若y1<0,y2>0,且a+b<0,则a>0.其中正确的结论个数为( )
A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com