
����Ŀ����ҵ����ˮ���������ַ�ʽ��һ�������͵���ˮ�����м��д�������һ����ͨ����ҵ�������豸���д�����ij��ҵȥ��ÿ�µ���ˮ����Ϊ12000�֣�������ˮ�����ڵ��ԽΣ���ˮ�����������ޣ�����ҵͶ���Խ��豸������ˮ�����ִ�����ʽͬʱ���У�1��6�£�����ҵ����ˮ�����͵���ˮ��y1���֣����·�x��1��x��6����xȡ������֮������ĺ�����ϵ���±���
�·�x���£� | 1 | 2 | 3 | 4 | 5 | 6 |
���͵���ˮ��y1���֣� | 12000 | 6000 | 4000 | 3000 | 2400 | 2000 |
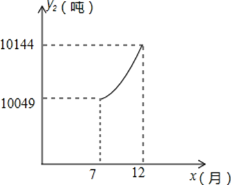
7��12�£�����ҵ������������ˮ��y2���֣����·�x��7��x��12����xȡ������֮��������κ�����ϵʽΪ![]() ��a��0������ͼ����ͼ��ʾ��1��6�£���ˮ������ÿ����ˮ�ķ��ã�z1��Ԫ�����·�x֮�����㺯����ϵʽ��
��a��0������ͼ����ͼ��ʾ��1��6�£���ˮ������ÿ����ˮ�ķ��ã�z1��Ԫ�����·�x֮�����㺯����ϵʽ��![]() ������ҵ��������ÿ����ˮ�ķ��ã�z2��Ԫ�����·�x֮�����㺯����ϵʽ��
������ҵ��������ÿ����ˮ�ķ��ã�z2��Ԫ�����·�x֮�����㺯����ϵʽ��![]() ��7��12�£���ˮ������ÿ����ˮ�ķ��þ�Ϊ2Ԫ������ҵ��������ÿ����ˮ�ķ��þ�Ϊ1.5Ԫ��
��7��12�£���ˮ������ÿ����ˮ�ķ��þ�Ϊ2Ԫ������ҵ��������ÿ����ˮ�ķ��þ�Ϊ1.5Ԫ��
��1����۲����еı����ͼ������ѧ����һ�κ�������������������κ������й�֪ʶ���ֱ�ֱ��д��y1��y2��x֮��ĺ�����ϵʽ��
��2�������������ҵȥ���ĸ���������ˮ�����ķ���W��Ԫ����࣬�������������ã�
��3�����������������Խ���ˮ�����豸��ȫ�����У�����ҵ����������ܲ���������ˮȫ����������������������ܺ����ÿ�µ���ˮ��������ȥ��ÿ�µĻ���������a%��ͬʱÿ����ˮ�����ķ��ý���ȥ��12�·ݵĻ��������ӣ�a-30��%��Ϊ�������ܽ��ģ�������ҵ��������������ҵ������ˮ�ķ��ý���50%�IJ�����������ҵÿ�µ���ˮ��������Ϊ18000Ԫ��������a������ֵ��
���ο����ݣ�![]() ��15.2��
��15.2��![]() ��20.5��
��20.5��![]() ��28.4��
��28.4��
���𰸡���1��y1=![]() ��1��x��6����xȡ��������y2=x2+10000��7��x��12����xȡ����������2��ȥ��5��������ˮ�����ķ�����࣬��������22000Ԫ����3��a��ֵ��57��
��1��x��6����xȡ��������y2=x2+10000��7��x��12����xȡ����������2��ȥ��5��������ˮ�����ķ�����࣬��������22000Ԫ����3��a��ֵ��57��
��������
��1�����ú���ͼ��ó���ͼ�����7��10049������12��10144���㣬�������ʽ���ɣ�
��2�����õ�7��x��12ʱ�����������ˮ�ķ��ã����ɵó��𰸣�
��3�����ý���ÿ�µ���ˮ��������ȥ��ÿ�µĻ���������a%��ͬʱÿ����ˮ�����ķ��ý���ȥ��12�·ݵĻ��������ӣ�aһ30��%���ó���ʽ12000��1+a%����1.5��[1+��a-30��%]����1-50%��=18000������������ɣ�
����1�����ݱ��������ݿ��Եó�xy=��ֵ����y1��x֮��ĺ�����ϵΪ������������ϵ��
y1=![]() ������1��12000������ã�
������1��12000������ã�
k=1��12000=12000��
��y1=![]() ��1��x��6����xȡ��������
��1��x��6����xȡ��������
����ͼ����Եó���ͼ�����7��10049������12��10144���㣬
����![]() �ã�
�ã�![]() ��
��
��ã�![]() ��
��
��y2=x2+10000��7��x��12����xȡ��������
��2����1��x��6����xȡ����ʱ��
![]() ��
��
=-1000x2+10000x-3000��
��a=-1000��0��x=-![]() =5��1��x��6��
=5��1��x��6��
�൱x=5ʱ��W���=22000��Ԫ����
��7��x��12ʱ����xȡ����ʱ��
W=2����12000-y2��+1.5y2=2����12000-x2-10000��+1.5��x2+10000����
=-![]() x2+19000��
x2+19000��
��a=-![]() ��0��x=-
��0��x=-![]() =0��
=0��
��7��x��12ʱ��W��x���������С��
�൱x=7ʱ��W���=18975.5��Ԫ����
��22000��18975.5��
��ȥ��5��������ˮ�����ķ�����࣬��������22000Ԫ��
��3��������ã�12000��1+a%����1.5��[1+��a-30��%]����1-50%��=18000��
��t=a%�������ã�10t2+17t-13=0��
��ã�t=![]() ��
��
��![]() ��28.4��
��28.4��
��t1��0.57��t2��-2.27����ȥ����
��a��57��
��a��ֵ��57��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���˽�ȫУ3000��ѧ����ѧУ���õ���������ƹ������ë����������������ϲ���������ȫУ��Χ�����������m��ѧ����ÿ��ѧ����ѡ��ֻ��ѡ���������е�һ�֣��������ʾ����飬��ͳ�����ݻ��Ƴ�����������������ͳ��ͼ�������ͳ��ͼ�ṩ����Ϣ������������⣺
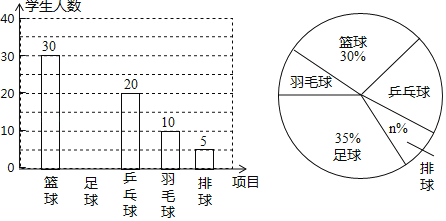
��1��m���� ����n���� ��������ȫͼ�е�����ͳ��ͼ��
��2��������Ƹ�УԼ�ж�����ѧ��ϲ����ƹ����
��3���ڳ���m��ѧ���У���A��B��C��D��10��ѧ��ϲ����ë����ѧУ�����A��B��C��D��4��Ů���У�ѡȡ2���μ�ȫ����ѧ��Ů����ë������������б�������״ͼ������ͬʱѡ��B��C�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
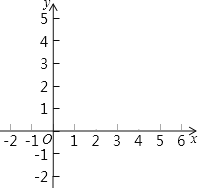
����Ŀ����ƽ��ֱ������ϵxOy�У�ֱ��y��kx+b(k��0)��������(6��0)������������Χ�ɵ������ε������9���뺯��y��![]() (x��0)��ͼ��G����A��B���㣮
(x��0)��ͼ��G����A��B���㣮
(1)��ֱ�ߵı���ʽ��
(2)�ᡢ�����궼�������ĵ�������㣮��ͼ��G�ڵ�A��B֮��IJ������߶�ABΧ�ɵ�����(�����߽�)ΪW��
����m��2ʱ��ֱ��д������W�ڵ������������ ����
��������W��ǡ��3�������㣬��Ϻ���ͼ����m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ٵ�һ�����ӣ�����һ���ֻ�!������2017����Ȧһƪ�ȴ������£������ϣ����������������� 2018 ��9����ѧ����Сѧ�ͳ��н�ֹѧ��ʹ���ֻ���Ϊ�˽�ѧ���ֻ�ʹ�������ijѧУ��չ�����ֻ����ҽ����������������������ȡ����ѧ��������ʹ���ֻ�Ŀ��������ÿ��ʹ���ֻ���ʱ�������ʾ����飬�����Ƴ���ͼ�٣��ڵ� ͳ��ͼ����֪������������������ 40�ˣ��������������Ϣ����������⣺
(1)������ͳ��ͼ�У�������Ϸ����Ӧ�İٷֱ�Ϊ______��Բ�ĽǶ�����______�ȣ�
(2)��ȫ����ͳ��ͼ��
(3)��У����ѧ��2100�ˣ�����ÿ��ʹ���ֻ�ʱ����2 Сʱ����(����2Сʱ)��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
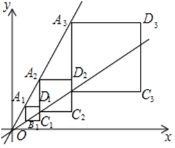
����Ŀ����ͼ����A1��1��![]() ����ֱ��y=kx�ϣ�����A1��A1B1��y�ύֱ��y=
����ֱ��y=kx�ϣ�����A1��A1B1��y�ύֱ��y=![]() x�ڵ�B1����A1B1Ϊ����A1B1���Ҳ���������A1B1C1D1��ֱ��C1D1�ֱ�ֱ��y=kx��y=
x�ڵ�B1����A1B1Ϊ����A1B1���Ҳ���������A1B1C1D1��ֱ��C1D1�ֱ�ֱ��y=kx��y=![]() x��A2��B2���㣬��A2B2Ϊ����A2B2���Ҳ�����������A2B2C2D2����ֱ��C2D2�ֱ�ֱ��y=kx��y=
x��A2��B2���㣬��A2B2Ϊ����A2B2���Ҳ�����������A2B2C2D2����ֱ��C2D2�ֱ�ֱ��y=kx��y=![]() x��A3��B3���㣬��A3B3Ϊ����A3B3���Ҳ���������A3B3C3D3���������˹��ɽ�����ȥ����������AnBnCnDn�����Ϊ____________�����ú�������n�Ĵ���ʽ��ʾ��
x��A3��B3���㣬��A3B3Ϊ����A3B3���Ҳ���������A3B3C3D3���������˹��ɽ�����ȥ����������AnBnCnDn�����Ϊ____________�����ú�������n�Ĵ���ʽ��ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ְ�����С��һ�������һ�����г���Ϊ��������ڼס������̳�������ͬ������г�������ͬ���������Ҳ��ͬ�����г����������֮��Ϊ452Ԫ�������г��ĵ��۱�����ĵ���4����8Ԫ��
��1�������г���������۸�Ϊ����Ԫ��
��2���������ٸ����̼Ҵ��������̳�������Ʒ������ۣ���8.5�ۣ����ۣ���ȫ�������100Ԫ������ȯ30Ԫ��������100Ԫ����ȯ����100Ԫ��30Ԫ����ȯ����200Ԫ��60Ԫ����ȯ�������ɵ������ڹ������ȯȫ��ͨ�ã����ְ�ֻ����400ԪǮ�������ֻ��ͬһ���̳������е�������Ʒ������һ�����ʡǮ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ߵ�����Ů��������е�һ��������Ŀ������������ɸߡ�������ƽ�иܼ�����֧����ɣ��˶�Ա�ɸ����Լ������ߺ�ϰ���ڹ涨��Χ�ڵ��ڸߡ������ܼ�ľ��룮ij��ȤС����ݸߵ����ĵ�һ�ֽ���ͼ������������ѧ���⣬������
��ͼ��ʾ��������A��B�����ľ���Ϊ90cm�����ϵ�C��ֱ��AB�ľ���CE�ij�Ϊ155cm���߸��ϵ�D��ֱ��AB�ľ���DF�ij�Ϊ234cm����֪�ܵ�֧��AC��ֱ��AB�ļнǡ�CAEΪ82.4�����߸ܵ�֧��BD��ֱ��AB�ļнǡ�DBFΪ80.3������ߡ��ܼ��ˮƽ����CH�ij����������ȷ��1cm���ο�����sin82.4���0.991��cos82.4���0.132��tan82.4���7.500��sin80.3���0.983��cos80.3���0.168��tan80.3���5.850��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
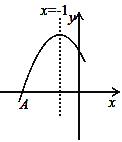
����Ŀ����ͼ�Ƕ��κ���y=ax2+bx+cͼ���һ���֣�ͼ�����A����3��0�����Գ���Ϊֱ��x=��1���������½��ۣ���abc��0 ��b2��4ac��0 ��4b+c��0 ����B����![]() ��y1����C����
��y1����C����![]() ��y2��Ϊ����ͼ���ϵ����㣬��y1��y2������3��x��1ʱ��y��0��
��y2��Ϊ����ͼ���ϵ����㣬��y1��y2������3��x��1ʱ��y��0��
������ȷ�Ľ����ǣ���д������ȷ���۵���ţ�__________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ѿ�֪��һЩ����Ĺ����������������������еĹ�������3��4��5������������ż���еĹ�����6��8��10����ʵ�ϣ�������������������Ȼ�ǹ�������
(1)��������һЩ���ɹ������Ĺ�ʽҲ����д������������ϴ����˹ѧ������Ĺ�ʽ��a��2n+1��b��2n2+2n��c��2n2+2n+1(nΪ������)��һ�鹴��������֤���������Ϲ�ʽ��a��b��c������һ�鹴������
(2)Ȼ���������ϵ�һ�θ����Ĺ�������ʽ���ռ����ҹ��Ŵ���������ѧ�����������������У������ᵽ����a��![]() (m2��n2)��b��mn��c��
(m2��n2)��b��mn��c��![]() (m2+n2)(m��nΪ��������m��nʱ��a��b��c����һ�鹴�����������������ۣ�����������⣺��֪ijֱ�������εı߳���������������������һ�߳�Ϊ37����n��5�����ֱ�������������ߵij���
(m2+n2)(m��nΪ��������m��nʱ��a��b��c����һ�鹴�����������������ۣ�����������⣺��֪ijֱ�������εı߳���������������������һ�߳�Ϊ37����n��5�����ֱ�������������ߵij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com