
����Ŀ�������Ѿ�֪��һЩ����Ĺ����������������������еĹ�������3��4��5������������ż���еĹ�����6��8��10����ʵ�ϣ�������������������Ȼ�ǹ�������
(1)��������һЩ���ɹ������Ĺ�ʽҲ����д������������ϴ����˹ѧ������Ĺ�ʽ��a��2n+1��b��2n2+2n��c��2n2+2n+1(nΪ������)��һ�鹴��������֤���������Ϲ�ʽ��a��b��c������һ�鹴������
(2)Ȼ���������ϵ�һ�θ����Ĺ�������ʽ���ռ����ҹ��Ŵ���������ѧ�����������������У������ᵽ����a��![]() (m2��n2)��b��mn��c��
(m2��n2)��b��mn��c��![]() (m2+n2)(m��nΪ��������m��nʱ��a��b��c����һ�鹴�����������������ۣ�����������⣺��֪ijֱ�������εı߳���������������������һ�߳�Ϊ37����n��5�����ֱ�������������ߵij���
(m2+n2)(m��nΪ��������m��nʱ��a��b��c����һ�鹴�����������������ۣ�����������⣺��֪ijֱ�������εı߳���������������������һ�߳�Ϊ37����n��5�����ֱ�������������ߵij���
���𰸡�(1)֤����������(2)��n��5ʱ��һ�߳�Ϊ37��ֱ�������������ߵij��ֱ�Ϊ12��35��
��������
��1����������ֻ��Ҫ֤��a2+b2��c2�����ɽ��
��2���������⽫n��5����õ�a��![]() (m2��52)��b��5m��c��
(m2��52)��b��5m��c��![]() (m2+25)���ٽ�ֱ�������ε�һ�߳�Ϊ37���ֱ�������������a��
(m2+25)���ٽ�ֱ�������ε�һ�߳�Ϊ37���ֱ�������������a��![]() (m2��52)��b��5m��c��
(m2��52)��b��5m��c��![]() (m2+25)�����ɽ��
(m2+25)�����ɽ��
(1)��a2+b2��(2n+1)2+(2n2+2n)2��4n2+4n+1+4n4+8n3+4n2��4n4+8n3+8n2+4n+1��
c2��(2n2+2n+1)2��4n4+8n3+8n2+4n+1��
��a2+b2��c2��
��n��������
��a��b��c��һ�鹴������
(2)�⣺��n��5
��a��![]() (m2��52)��b��5m��c��
(m2��52)��b��5m��c��![]() (m2+25)��
(m2+25)��
��ֱ�������ε�һ�߳�Ϊ37��
�������������ۣ�
�ٵ�a��37ʱ��![]() (m2��52)��37��
(m2��52)��37��
���m����3![]() (�������⣬��ȥ)
(�������⣬��ȥ)
�ڵ�y��37ʱ��5m��37��
���m��![]() (����������ȥ)��
(����������ȥ)��
�۵�z��37ʱ��37��![]() (m2+n2)��
(m2+n2)��
���m����7��
��m��n��0��m��n�ǻ��ʵ�������
��m��7��
��m��7����٢ڵã�x��12��y��35��
������������n��5ʱ��һ�߳�Ϊ37��ֱ�������������ߵij��ֱ�Ϊ12��35��


 �߲������Ӧ��һ��ͨϵ�д�
�߲������Ӧ��һ��ͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�������y����x2+2tx+2��
��1���������ߵĶԳ��ᣨ�ú�t�Ĵ���ʽ��ʾ����
��2������A����1��3������ƽ��5����λ���ȣ��õ���B��
���������߾�����B��t��ֵ��
�������������߶�ABǡ��һ�����㣬��Ϻ���ͼ��ֱ��д��t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
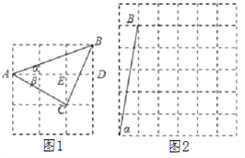
����Ŀ��(1)��ͼ1����������¶�Ϊ��ǣ���tan��=![]() ��tan��=
��tan��=![]() ����+��=___________��
����+��=___________��
(2)��������¶�Ϊ��ǣ���tan��=5��tan��=![]() ʱ����ͼ2�������������У���������������Ǩ���������MON��ʹ�á�MON=��-��.��ʱ��-��=__________��.
ʱ����ͼ2�������������У���������������Ǩ���������MON��ʹ�á�MON=��-��.��ʱ��-��=__________��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������һ���ߵı߳�Ϊ3�������������ߵı߳��ǹ���x��һԪ���η���x2��12x+k=0������������k��ֵ��________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
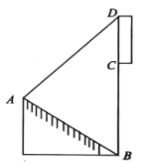
����Ŀ��С����ij��б��![]() �ϣ���������ij��¥
�ϣ���������ij��¥![]() �Ϸ���һ���˴����й����ʽ��ڲ�����������ֱ������
�Ϸ���һ���˴����й����ʽ��ڲ�����������ֱ������![]() ��С����
��С����![]() ���ñ����ƶ���D��������Ϊ
���ñ����ƶ���D��������Ϊ![]() �����Ҳ��б��
�����Ҳ��б��![]() ���¶�Ϊ
���¶�Ϊ![]() ��
��![]() ��ͬһ��ֱ���ϣ�����֪б��
��ͬһ��ֱ���ϣ�����֪б��![]() ��
��![]() �ף���¥��
�ף���¥��![]() �ף���
�ף���![]() �ף����������
�ף����������![]() �ij��ǣ� ���ף����������С�����һλ�����ο����ݣ�
�ij��ǣ� ���ף����������С�����һλ�����ο����ݣ�![]() ��
�� ![]() ��
�� ![]() ��
��![]() ��
��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ��չ�����ֻ����ҽ����������������������ȡ����ѧ���������ֻ�ʹ��Ŀ��������ÿ��ʹ���ֻ�ʱ�������ʾ����飬�����Ƴ���ͼ������ͳ��ͼ����֪������������������40�ˡ�
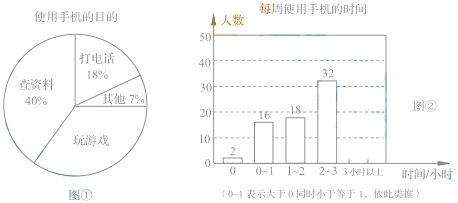
�������������Ϣ�����������
��1��������ͳ��ͼ�У�������Ϸ����Ӧ��Բ�ĽǶ�����_______________��
��2����ȫ����ͳ��ͼ
��3����У����ѧ��1200�ˣ�����ÿ��ʹ���ֻ�ʱ����2Сʱ���ϣ�����2Сʱ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
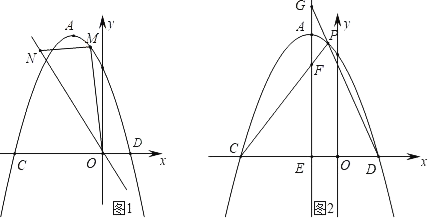
����Ŀ����ƽ��ֱ������ϵ�У���֪�����ߵĶ���ΪA����1��4�����Ҿ�����B����2��3������x��քe����C��D���㣨��C�ڵ�D����ࣩ��
��1����������߶�Ӧ�ĺ�������ʽ��
��2����ͼ1����M���������ϵ�һ�����㣬����ֱ��OB���Ϸ�������M��x���ƽ������ֱ��OB���ڵ�N������OM��
����MN�����ֵ��
�ڵ���OMNΪֱ��������ʱ��ֱ��д����M�����ꣻ
��3����ͼ2������A��ֱ�߽�x���ڵ�E����AE��y�ᣬ��P����������A��D֮���һ�����㣬ֱ��PC��PD��AE�քe����F��G���㣮����P�˶�ʱ��EF+EG�ĺ��Ƿ�Ϊ��ֵ�����ǣ�������ö�ֵ�������ǣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�������![]() ��m>0����x�ύ��A��B���㣬��B�ڵ�A���Ҳ࣬����ΪC����������y�ύ�ڵ�D��ֱ��CA��y����E����
��m>0����x�ύ��A��B���㣬��B�ڵ�A���Ҳ࣬����ΪC����������y�ύ�ڵ�D��ֱ��CA��y����E����![]() ��
��
��1�����A����B�����ꣻ
��2������BCO�Ƶ�C��ʱ����תһ���ǶȺ�B���A�غϣ���Oǡ������y���ϣ�
����ֱ��CE�Ľ���ʽ��
���������ߵĽ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=kx��k��0����˫����y=![]() ����A��B���㣬BC��x����C������AC��y����D�����н��ۣ���A��B����ԭ��Գƣ��ڡ�ABC�����Ϊ��ֵ����D��AC���е㣻��S��AOD=
����A��B���㣬BC��x����C������AC��y����D�����н��ۣ���A��B����ԭ��Գƣ��ڡ�ABC�����Ϊ��ֵ����D��AC���е㣻��S��AOD=![]() ��������ȷ���۵ĸ���Ϊ�� ��
��������ȷ���۵ĸ���Ϊ�� ��
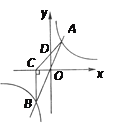
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com