
【题目】如图,直线y=kx(k>0)与双曲线y=![]() 交于A、B两点,BC⊥x轴于C,连接AC交y轴于D,下列结论:①A、B关于原点对称;②△ABC的面积为定值;③D是AC的中点;④S△AOD=
交于A、B两点,BC⊥x轴于C,连接AC交y轴于D,下列结论:①A、B关于原点对称;②△ABC的面积为定值;③D是AC的中点;④S△AOD=![]() .其中正确结论的个数为( )
.其中正确结论的个数为( )
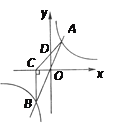
A.1个B.2个C.3个D.4个
科目:初中数学 来源: 题型:
【题目】我们已经知道一些特殊的勾股数,如三连续正整数中的勾股数:3、4、5;三个连续的偶数中的勾股数6、8、10;事实上,勾股数的正整数倍仍然是勾股数.
(1)另外利用一些构成勾股数的公式也可以写出许多勾股数,毕达哥拉斯学派提出的公式:a=2n+1,b=2n2+2n,c=2n2+2n+1(n为正整数)是一组勾股数,请证明满足以上公式的a、b、c的数是一组勾股数.
(2)然而,世界上第一次给出的勾股数公式,收集在我国古代的着名数学着作《九章算术》中,书中提到:当a=![]() (m2﹣n2),b=mn,c=
(m2﹣n2),b=mn,c=![]() (m2+n2)(m、n为正整数,m>n时,a、b、c构成一组勾股数;利用上述结论,解决如下问题:已知某直角三角形的边长满足上述勾股数,其中一边长为37,且n=5,求该直角三角形另两边的长.
(m2+n2)(m、n为正整数,m>n时,a、b、c构成一组勾股数;利用上述结论,解决如下问题:已知某直角三角形的边长满足上述勾股数,其中一边长为37,且n=5,求该直角三角形另两边的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
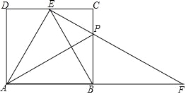
【题目】如图,在矩形ABCD中,AB=2,AD=![]() ,在边CD上有一点E,使EB平分∠AEC.若P为BC边上一点,且BP=2CP,连接EP并延长交AB的延长线于F.给出以下五个结论:
,在边CD上有一点E,使EB平分∠AEC.若P为BC边上一点,且BP=2CP,连接EP并延长交AB的延长线于F.给出以下五个结论:
①点B平分线段AF;②PF=![]() DE;③∠BEF=∠FEC;④S矩形ABCD=4S△BPF;⑤△AEB是正三角形.
DE;③∠BEF=∠FEC;④S矩形ABCD=4S△BPF;⑤△AEB是正三角形.
其中正确结论的序号是.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在Rt△ABC中,∠C=90°,AD是∠BAC的角平分线,以AB上一点O为圆心,AD为弦作⊙O.
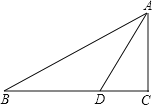
(1)用直尺和圆规在图中作出⊙O(不写作法,保留作图痕迹),判断直线BC与⊙O的位置关系,并说明理由;(友情提醒:必须作在答题卷上哦!)
(2)若AC=3,BC=4,求⊙O的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在Rt△ABC中,∠C=90°,AD是∠BAC的角平分线,以AB上一点O为圆心,AD为弦作⊙O.
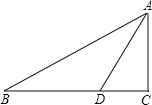
(1)用直尺和圆规在图中作出⊙O(不写作法,保留作图痕迹),判断直线BC与⊙O的位置关系,并说明理由;(友情提醒:必须作在答题卷上哦!)
(2)若AC=3,BC=4,求⊙O的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
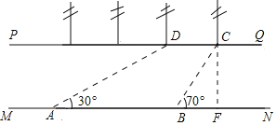
【题目】如图,河流两岸PQ,MN互相平行,C、D是河岸PQ上间隔50m的两个电线杆,某人在河岸MN上的A处测得∠DAB=30°,然后沿河岸走了100m到达B处,测得∠CBF=70°,求河流的宽度(结果精确到个位,![]() =1.73,sin70°=0.94,cos70°=0.34,tan70°=2.75)
=1.73,sin70°=0.94,cos70°=0.34,tan70°=2.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组![]() 请结合题意填空,完成本题的解答.
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得 ;
(Ⅱ)解不等式②,得 ;
(Ⅲ)把不等式①和②的解集在数轴上表示出来.
![]()
(Ⅳ)原不等式组的解集为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC的度数是( )
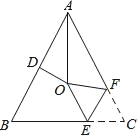
A. 106°B. 108°C. 110°D. 112°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com