
【题目】已知在Rt△ABC中,∠C=90°,AD是∠BAC的角平分线,以AB上一点O为圆心,AD为弦作⊙O.
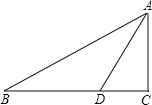
(1)用直尺和圆规在图中作出⊙O(不写作法,保留作图痕迹),判断直线BC与⊙O的位置关系,并说明理由;(友情提醒:必须作在答题卷上哦!)
(2)若AC=3,BC=4,求⊙O的半径长.
【答案】(1)图见解析,直线BC与⊙O相切,理由见解析;(2)![]()
【解析】
(1)因为AD是弦,所以圆心O即在AB上,也在AD的垂直平分线上,据此作图即可;因为D在圆上,所以只要能证明OD⊥BC就说明BC为⊙O的切线;
(2)设⊙O的半径为x,证△BOD∽△BAC得![]() ,即
,即![]() ,解之可得.
,解之可得.
解:(1)直线BC与⊙O相切.理由如下:
作图如图所示,连接OD,
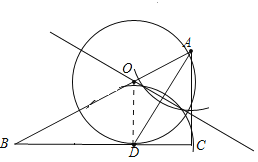
∵AD为角平分线,
∴∠OAD=∠CAD,
又∵OA=OD,
∴∠OAD=∠ODA,
∴∠CAD=∠ODA,
∴OD∥AC,
∵AC⊥BC,
∴OD⊥BC,
∴直线BC与⊙O相切;
(2)设⊙O的半径为x,
∵AC=3,BC=4,
∵AB=5,
又OD⊥BC,则OD∥BC,
∴△BOD∽△BAC,
∴![]() ,
,
即![]() ,
,
解得x=![]() ,
,
∴⊙O的半径为![]() .
.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:
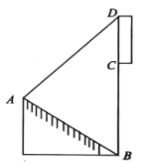
【题目】小明在某个斜坡![]() 上,看到对面某高楼
上,看到对面某高楼![]() 上方有一块宜传“中国国际进口博览会”的竖直标语牌
上方有一块宜传“中国国际进口博览会”的竖直标语牌![]() .小明在
.小明在![]() 点测得标语牌顶端D处的仰角为
点测得标语牌顶端D处的仰角为![]() ,并且测得斜坡
,并且测得斜坡![]() 的坡度为
的坡度为![]() (
(![]() 在同一条直线上),已知斜坡
在同一条直线上),已知斜坡![]() 长
长![]() 米,高楼高
米,高楼高![]() 米(即
米(即![]() 米),则标语牌
米),则标语牌![]() 的长是( )米.(结果保留小数点后一位)(参考数据:
的长是( )米.(结果保留小数点后一位)(参考数据:![]() ,
, ![]() ,
, ![]() ,
,![]() )
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
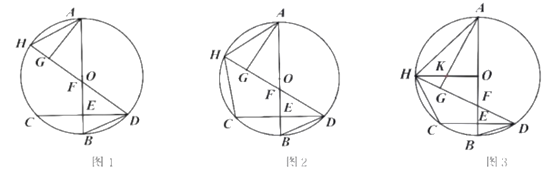
【题目】已知:如图,AB为![]() 的直径,弦
的直径,弦![]() 垂足为E,点H为弧AC上一点.连接DH交AB于点F,连接HA、BD,点G为DH上一点,连接AG,
垂足为E,点H为弧AC上一点.连接DH交AB于点F,连接HA、BD,点G为DH上一点,连接AG,![]() .
.
(1)如图1,求证:![]() ;
;
(2)如图2,连接HC,若![]() ,求证:
,求证:![]() ;
;
(3)如图3,连接![]() 交
交![]() 于点K,若点F为DG的中点,
于点K,若点F为DG的中点,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
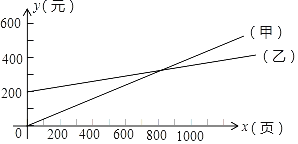
【题目】某学校有一批复印任务,原来由甲复印店承接,按每100页40元计费.现乙复印店表示:若学校先按月付给一定数额的承包费,则可按每100页15元收费.两复印店每月收费情况如图所示.
(1)乙复印店的每月承包费是多少元?
(2)当每月复印多少页时两复印店实际收费相同,费用是多少元?
(3)求甲、乙复印店的函数表达式.
(4)如果每月复印页数在1200页左右,那么应选择哪家复印店更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB是半圆O的直径,AC是弦,点P沿BA方向,从点B运动到点A,速度为1cm/s,若AB=10cm,点O到AC的距离为4cm.
(1)求弦AC的长;
(2)问经过多长时间后,△APC是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
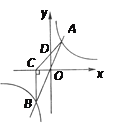
【题目】如图,直线y=kx(k>0)与双曲线y=![]() 交于A、B两点,BC⊥x轴于C,连接AC交y轴于D,下列结论:①A、B关于原点对称;②△ABC的面积为定值;③D是AC的中点;④S△AOD=
交于A、B两点,BC⊥x轴于C,连接AC交y轴于D,下列结论:①A、B关于原点对称;②△ABC的面积为定值;③D是AC的中点;④S△AOD=![]() .其中正确结论的个数为( )
.其中正确结论的个数为( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知y是x(x>0)的函数,表1中给出了几组x与y的对应值:
表1:
x | … |
| 1 |
| 2 |
| 3 | … |
y | … | 6 | 3 | 2 |
|
| 1 | … |
⑴以表中各对对应值为坐标,在图1的直角坐标系中描出各点,用光滑曲线顺次连接.由图像知,它是我们已经学过的哪类函数?求出函数解析式,并直接写出![]() 的值;
的值;
⑵如果一次函数图像与⑴中图像交于(1,3)和(3,1)两点,在第一、四象限内当x在什么范围时,一次函数的值小于⑴中函数的值?请直接写出答案.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明想测量电线杆AB的高度,但在太阳光下,电线杆的影子恰好落在地面和土地的坡面上,量得坡面上的影长CD=4m,地面上的影长BC=10m,土坡坡面与地面成30°的角,此时测得1m长的木杆的影长为2m,求电线杆的高度.(结果精确到0.1m)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D为AB中点,AE∥CD,CE∥AB.
(1)试判断四边形ADCE的形状,并证明你的结论.
(2)连接BE,若∠BAC=30°,CE=1,求BE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com