
【题目】在平面直角坐标系中,抛物线![]() (m>0)与x轴交于A,B两点,点B在点A的右侧,顶点为C,抛物线与y轴交于点D,直线CA交y轴于E,且
(m>0)与x轴交于A,B两点,点B在点A的右侧,顶点为C,抛物线与y轴交于点D,直线CA交y轴于E,且![]() .
.
(1)求点A,点B的坐标;
(2)将△BCO绕点C逆时针旋转一定角度后,点B与点A重合,点O恰好落在y轴上,
①求直线CE的解析式;
②求抛物线的解析式.
【答案】(1) A(![]() ,0) B(
,0) B(![]() ,0);(2) ①
,0);(2) ①![]() ,②
,②![]() .
.
【解析】
(1)根据抛物线的解析式可得对称轴为x=2,利用![]() 得出CA:CE=3:4,由△AOE∽△AGC可得
得出CA:CE=3:4,由△AOE∽△AGC可得![]() ,进而求得OA、OB的长,即可求得点A、点B的坐标;
,进而求得OA、OB的长,即可求得点A、点B的坐标;
(2)根据旋转的性质求出C点坐标,利用C点坐标和△AOE∽△AGC可求得E点坐标,,分别利用待定系数法即可求得直线CE和抛物线的解析式.
解:(1)∵抛物线的解析式为![]() ,
,
∴对称轴为直线![]() ,
,
如图,设对称轴与x轴交于G,则![]() 轴,
轴,![]() ,
,
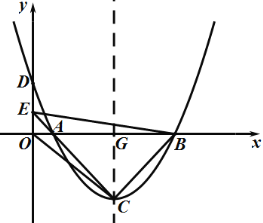
∴△AOE∽△AGC,
∴![]() ,
,
∵![]() ,
,
∴CA:CE=3:4 ,则![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
∴A(![]() ,0), B(
,0), B(![]() ,0);
,0);
(2)如图,设O旋转后落在点Q处,过点C作![]() 轴于点P,
轴于点P,
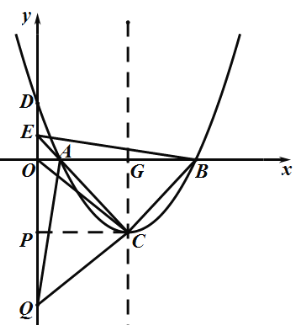
由旋转的性质得:△BCO≌△ACQ,
∴BO=AQ=![]() ,CO=CQ,
,CO=CQ,
∴OQ=![]() ,
,
∵![]() 轴,
轴,
∴![]() ,
,
∴点C的坐标为![]() ,则
,则![]()
由(1)得△AOE∽△AGC,![]() ,
,
∴![]() ,即点E的坐标为
,即点E的坐标为![]() ,
,
①设CE的解析式为![]() ,分别代入C
,分别代入C![]() ,E
,E![]() 得:
得:
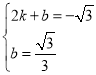 ,解得:
,解得: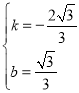 ,
,
∴CE的解析式为![]() ;
;
②将A(![]() ,0),C
,0),C![]() 分别代入
分别代入![]() 得:
得:
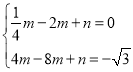 ,解得:
,解得: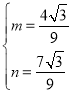 ,
,
∴抛物线解析式为![]() .
.


科目:初中数学 来源: 题型:
【题目】课题研究小组对附着在物体表面的三个微生物(课题小组成员把他们分别标号为1,2,3)的生长情况进行观察记录.这三个微生物第一天各自一分为二,产生新的微生物(分别被标号为4,5,6,7,8,9),接下去每天都按照这样的规律变化,即每个微生物一分为二,形成新的微生物(课题组成员用如图所示的图形进行形象的记录).那么标号为100的微生物会出现在( )
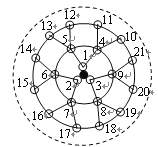
A.第3天B.第4天C.第5天D.第6天
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们已经知道一些特殊的勾股数,如三连续正整数中的勾股数:3、4、5;三个连续的偶数中的勾股数6、8、10;事实上,勾股数的正整数倍仍然是勾股数.
(1)另外利用一些构成勾股数的公式也可以写出许多勾股数,毕达哥拉斯学派提出的公式:a=2n+1,b=2n2+2n,c=2n2+2n+1(n为正整数)是一组勾股数,请证明满足以上公式的a、b、c的数是一组勾股数.
(2)然而,世界上第一次给出的勾股数公式,收集在我国古代的着名数学着作《九章算术》中,书中提到:当a=![]() (m2﹣n2),b=mn,c=
(m2﹣n2),b=mn,c=![]() (m2+n2)(m、n为正整数,m>n时,a、b、c构成一组勾股数;利用上述结论,解决如下问题:已知某直角三角形的边长满足上述勾股数,其中一边长为37,且n=5,求该直角三角形另两边的长.
(m2+n2)(m、n为正整数,m>n时,a、b、c构成一组勾股数;利用上述结论,解决如下问题:已知某直角三角形的边长满足上述勾股数,其中一边长为37,且n=5,求该直角三角形另两边的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
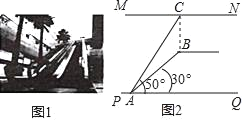
【题目】如图1是某商场从一楼到二楼的自动扶梯,图2是侧面示意图,MN是二楼楼顶,MN∥PQ,点C在MN上,且位于自动扶梯顶端B点的正上方,BC⊥MN.测得AB=10米,在自动扶梯底端A处测得点C的仰角为50°,点B的仰角为30°,求二楼的层高BC(结果保留根号)
(参考数据:sin50°=0.77,cos50°=0.64,tan50°=1.20)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中考体育测试前,某区教育局为了了解选报引体向上的初三男生的成绩情况,随机抽取了本区部分选报引体向上项目的初三男生的成绩,并将测试得到的成绩绘成了下面两幅不完整的统计图:

请你根据图中的信息,解答下列问题:
(1)写出扇形图中![]() ______,并补全条形图;
______,并补全条形图;
(2)样本数据的平均数是______,众数是______,中位数是______;
(3)该区体育中考选报引体向上的男生共有1200人,如果体育中考引体向上达6个以上(含6个)得满分,请你估计该区体育中考中选报引体向上的男生能获得满分的有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
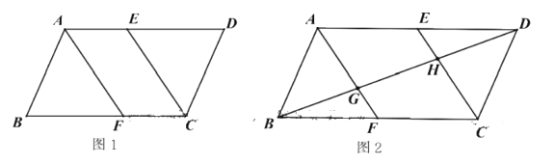
【题目】已知平行四边形ABCD,连接AF,CE、AF平分![]() 交BC于点F,CE平分
交BC于点F,CE平分![]() 交AD于点E.
交AD于点E.
(1)如图1,求证:四边形AFCE为平行四边形;
(2)如图2,连接BD,分别交AF、CE于G、H,若![]() ,在不添加其他辅助线的情况下,直接找出图中面积为平行四边形ABCD面积的
,在不添加其他辅助线的情况下,直接找出图中面积为平行四边形ABCD面积的![]() 的三角形或四边形.
的三角形或四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
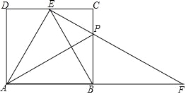
【题目】如图,在矩形ABCD中,AB=2,AD=![]() ,在边CD上有一点E,使EB平分∠AEC.若P为BC边上一点,且BP=2CP,连接EP并延长交AB的延长线于F.给出以下五个结论:
,在边CD上有一点E,使EB平分∠AEC.若P为BC边上一点,且BP=2CP,连接EP并延长交AB的延长线于F.给出以下五个结论:
①点B平分线段AF;②PF=![]() DE;③∠BEF=∠FEC;④S矩形ABCD=4S△BPF;⑤△AEB是正三角形.
DE;③∠BEF=∠FEC;④S矩形ABCD=4S△BPF;⑤△AEB是正三角形.
其中正确结论的序号是.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在Rt△ABC中,∠C=90°,AD是∠BAC的角平分线,以AB上一点O为圆心,AD为弦作⊙O.
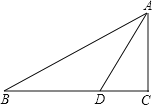
(1)用直尺和圆规在图中作出⊙O(不写作法,保留作图痕迹),判断直线BC与⊙O的位置关系,并说明理由;(友情提醒:必须作在答题卷上哦!)
(2)若AC=3,BC=4,求⊙O的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC的度数是( )
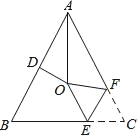
A. 106°B. 108°C. 110°D. 112°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com