
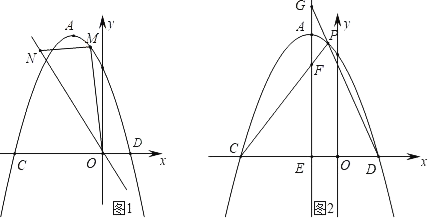
����Ŀ����ƽ��ֱ������ϵ�У���֪�����ߵĶ���ΪA����1��4�����Ҿ�����B����2��3������x��քe����C��D���㣨��C�ڵ�D����ࣩ��
��1����������߶�Ӧ�ĺ�������ʽ��
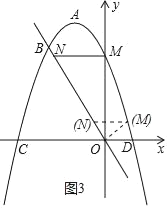
��2����ͼ1����M���������ϵ�һ�����㣬����ֱ��OB���Ϸ�������M��x���ƽ������ֱ��OB���ڵ�N������OM��
����MN�����ֵ��
�ڵ���OMNΪֱ��������ʱ��ֱ��д����M�����ꣻ
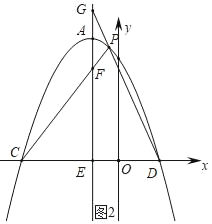
��3����ͼ2������A��ֱ�߽�x���ڵ�E����AE��y�ᣬ��P����������A��D֮���һ�����㣬ֱ��PC��PD��AE�քe����F��G���㣮����P�˶�ʱ��EF+EG�ĺ��Ƿ�Ϊ��ֵ�����ǣ�������ö�ֵ�������ǣ���˵�����ɣ�
���𰸡���1��y����x2��2x+3����2����![]() ���ڵ�M������Ϊ��0��3����
���ڵ�M������Ϊ��0��3����![]() ������3��EF+EG�ĺ�Ϊ��ֵ���ö�ֵΪ8�����ɼ�����
������3��EF+EG�ĺ�Ϊ��ֵ���ö�ֵΪ8�����ɼ�����
��������
��1���������ߵĶ���������������߶�Ӧ�ĺ�������ʽΪy��a��x+1��2+4�������B����������aֵ�������ɵó������߶�Ӧ�ĺ�������ʽ��
��2�����ɵ�B���������ô���ϵ�����ɵó�ֱ��OB�ĺ�������ʽ������ֱ��OB�������ߵĺ�������ʽ�ɷ����飬ͨ���ⷽ��������ֱ�ߺ������ߵĽ������꣬���M������Ϊ��m����m2��2m+3������2��m��![]() �������N������Ϊ��
�������N������Ϊ��![]() ����m2��2m+3���������ɵó�MN��
����m2��2m+3���������ɵó�MN��![]() �������ö��κ��������ʼ��ɽ����ֵ���⣻
�������ö��κ��������ʼ��ɽ����ֵ���⣻
����MN��x���֪��ONM��90�㣬�֡�OMN��90��͡�MON��90������������ǣ���i������OMN��90��ʱ���߶�OM��y���ϣ����ö��κ���ͼ���ϵ�������������������M�����ꣻ��ii������MON��90��ʱ��OM��OB���ɵ�B������ɵó�ֱ��OM���㣨3��2���������ɵó�ֱ��OM��Ӧ�ĺ�������ʽ������ֱ��OM�������ߵĺ�������ʽ�ɷ����飬ͨ���ⷽ����������M�����ꣻ
��3�����ö��κ���ͼ���ϵ�����������������C��D�����꣬���P������Ϊ��n����n2��2n+3������1��n��1�������ô���ϵ���������ֱ��CP��DP��Ӧ�ĺ�������ʽ���ɵ�A��������AE��y��ɵó�ֱ��AE��Ӧ�ĺ�������ʽ������һ�κ���ͼ���ϵ�����������������F��G�����꣬�����ɵó�EF��EG��EF+EG��ֵ��
��1���������ߵĶ���ΪA����1��4����
���������߶�Ӧ�ĺ�������ʽΪy��a��x+1��2+4��
��B����2��3������y��a��x+1��2+4���ã�3��a+4��
��ã�a����1��
�������߶�Ӧ�ĺ�������ʽΪy������x+1��2+4����y����x2��2x+3��
��2������ֱ��OB��Ӧ�ĺ�������ʽΪy��kx��k��0����
��B����2��3������y��kx���ã�3����2k��
��ã�k����![]() ��
��
��ֱ��OB��Ӧ�ĺ�������ʽΪy����![]() x��
x��
����ֱ��OB�������ߵĺ�������ʽ�ɷ����飬�ã�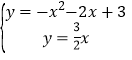 ��
��
��ã�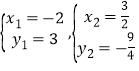 ��
��
���M��������m����m2��2m+3������2��m��![]() �������N��������
�������N��������![]() m2+
m2+![]() m��2����m2��2m+3����
m��2����m2��2m+3����
��MN��m����![]() m2+
m2+![]() m��2������
m��2������![]() m2��
m2��![]() m+2����
m+2����![]() ��m+
��m+![]() ��2+
��2+![]() ��
��
�ߩ�![]() ��0��
��0��
�൱m����![]() ʱ��MN������ֵΪ
ʱ��MN������ֵΪ![]() ��
��
�ڡ�MN��x�ᣬ
���ONM��90����
�������������ǣ���ͼ3��������
��i������OMN��90��ʱ���߶�OM��y���ϣ�
�ߵ�m��0ʱ��y����m2��2m+3��3��
���M��������0��3����
��ii������MON��90��ʱ��OM��OB��
�ߵ�B������Ϊ����2��3����
��㣨3��2����ֱ��OM�ϣ�
��ֱ��OM��Ӧ�ĺ�������ʽΪy��![]() x��
x��
����ֱ��OM�������ߵĺ�������ʽ�ɷ����飬�ã�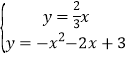 ��
��
��ã�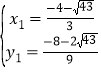 ���������⣬��ȥ����
���������⣬��ȥ����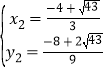 ��
��
���M��������![]() ����
����
������������M��������0��3����![]() ����
����
��3����y��0ʱ����x2��2x+3��0��
��ã�x1����3��x2��1��
���C����������3��0������D��������1��0����
���P��������n����n2��2n+3������1��n��1����
�ߵ�C������Ϊ����3��0������D������Ϊ��1��0����
��ֱ��CP��Ӧ�ĺ�������ʽΪy����1��n��x+3��3n��ֱ��DP��Ӧ�ĺ�������ʽΪy������n+3��x+n+3�������ô���ϵ�����������
�ߵ�A������Ϊ����1��4����AE��y�ᣬ
��ֱ��AE��Ӧ�ĺ�������ʽΪx����1��
��x����1ʱ��y����1��n��x+3��3n��2��2n��y������n+3��x+n+3��2n+6��
���F����������1��2��2n������G����������1��2n+6����
��EF��2��2n��EG��2n+6��
��EF+EG��8��
��EF+EG�ĺ�Ϊ��ֵ���ö�ֵΪ8��


 �����Ծ���ĩ���100��ϵ�д�
�����Ծ���ĩ���100��ϵ�д� ˫��ͬ������ѵ��ϵ�д�
˫��ͬ������ѵ��ϵ�д� �Ƹ�С״Ԫͬ������������ϵ�д�
�Ƹ�С״Ԫͬ������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��ij���ֻ������еĸ������ͳ�����������ͼ�����������ͼ����Ϣ������и��⣺
��Ŀ | �¹��ܷ� | �������� | ��;���� | ���ŷ� |
���/Ԫ | 5 | �� | �� | 25 |
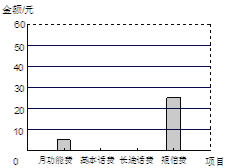
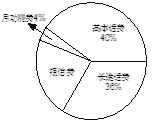
��1������С���ֻ����ѹ��ж���Ԫ��
��2������ͳ��ͼ�У���ʾ���ŷѵ����ε�Բ�Ľ�Ϊ���ٶȣ�
��3���뽫����������
��4���뽫����ͳ��ͼ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Ϊ����ɫ������������������ղ����ᣬ����2019��4��29����2019��10��7�����й����������������У��ݽ��ܣ��ڹ��ʾ��������ٰ�ĵ�����������¼���������ԡ��辰���ջ�����ר����ʾ���(����ֲ������Ϊ��λ)��
��1����μӾ����Ĺ��ж�����ֲ�
��2����ȫƵ���ֲ�ֱ��ͼ��
��3���Ӳ�����Ʒ����ѡһ��ֲ����¼������ԡ��ĸ��ʣ�
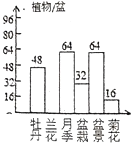 ��������
��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ѿ�֪��һЩ����Ĺ����������������������еĹ�������3��4��5������������ż���еĹ�����6��8��10����ʵ�ϣ�������������������Ȼ�ǹ�������
(1)��������һЩ���ɹ������Ĺ�ʽҲ����д������������ϴ����˹ѧ������Ĺ�ʽ��a��2n+1��b��2n2+2n��c��2n2+2n+1(nΪ������)��һ�鹴��������֤���������Ϲ�ʽ��a��b��c������һ�鹴������
(2)Ȼ���������ϵ�һ�θ����Ĺ�������ʽ���ռ����ҹ��Ŵ���������ѧ�����������������У������ᵽ����a��![]() (m2��n2)��b��mn��c��
(m2��n2)��b��mn��c��![]() (m2+n2)(m��nΪ��������m��nʱ��a��b��c����һ�鹴�����������������ۣ�����������⣺��֪ijֱ�������εı߳���������������������һ�߳�Ϊ37����n��5�����ֱ�������������ߵij���
(m2+n2)(m��nΪ��������m��nʱ��a��b��c����һ�鹴�����������������ۣ�����������⣺��֪ijֱ�������εı߳���������������������һ�߳�Ϊ37����n��5�����ֱ�������������ߵij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
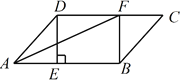
����Ŀ����ͼ����ƽ���ı���![]() �У�����
������![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() �ڱ�
�ڱ�![]() �ϣ�
�ϣ�![]() ������
������![]() ��
��![]() ��
��
(1)��֤���ı���BFDE�Ǿ��Σ�
(2)��CF=3��BE=5��AFƽ����DAB����ƽ���ı���![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
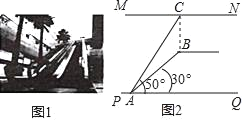
����Ŀ����ͼ1��ij�̳���һ¥����¥���Զ����ݣ�ͼ2�Dz���ʾ��ͼ��MN�Ƕ�¥¥����MN��PQ����C��MN�ϣ���λ���Զ����ݶ���B������Ϸ���BC��MN�����AB��10�ף����Զ����ݵ�A����õ�C������Ϊ50������B������Ϊ30�������¥�IJ��BC������������ţ�
���ο����ݣ�sin50����0.77��cos50����0.64��tan50����1.20��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���п���������ǰ��ij��������Ϊ���˽�ѡ���������ϵij��������ijɼ�����������ȡ�˱�������ѡ������������Ŀ�ij��������ijɼ����������Եõ��ijɼ����������������������ͳ��ͼ��

�������ͼ�е���Ϣ������������⣺
��1��д������ͼ��![]() ______������ȫ����ͼ��
______������ȫ����ͼ��
��2���������ݵ�ƽ������______��������______����λ����______��
��3�����������п�ѡ���������ϵ���������1200�ˣ���������п��������ϴ�6�����ϣ���6���������֣�������Ƹ��������п���ѡ���������ϵ������ܻ�����ֵ��ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
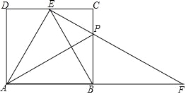
����Ŀ����ͼ���ھ���ABCD�У�AB=2��AD=![]() ���ڱ�CD����һ��E��ʹEBƽ�֡�AEC����PΪBC����һ�㣬��BP=2CP������EP���ӳ���AB���ӳ�����F����������������ۣ�
���ڱ�CD����һ��E��ʹEBƽ�֡�AEC����PΪBC����һ�㣬��BP=2CP������EP���ӳ���AB���ӳ�����F����������������ۣ�
�ٵ�Bƽ���߶�AF����PF=![]() DE���ۡ�BEF=��FEC����S����ABCD=4S��BPF���ݡ�AEB���������Σ�
DE���ۡ�BEF=��FEC����S����ABCD=4S��BPF���ݡ�AEB���������Σ�
������ȷ���۵�����ǣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ⲻ��ʽ��![]() ����������գ���ɱ���Ľ��
����������գ���ɱ���Ľ��
�������ⲻ��ʽ�������� ����
�������ⲻ��ʽ�������� ����
�������Ѳ���ʽ�������Ľ⼯�������ϱ�ʾ������
![]()
������ԭ����ʽ��Ľ⼯Ϊ�� ����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com