
°ĺŐ‚ńŅ°Ņő™ŃňŃňĹ‚»ę–£3000√Ż—ß…ķ∂‘—ß–£…Ť÷√Ķń◊„«Ú°Ęņļ«Ú°Ę∆ĻŇ“«Ú°Ę”ū√ę«Ú°ĘŇŇ«ÚĻ≤őŚŌÓ«ÚņŗĽÓ∂ĮĶńŌ≤įģ«ťŅŲ£¨‘ŕ»ę–£∑∂őßńŕňśĽķĶų≤ťŃňm√Ż—ß…ķ£®√Ņ√Ż—ß…ķĪō—°«“÷Ľń‹—°‘Ů’‚őŚŌÓĽÓ∂Į÷–Ķń“Ľ÷÷£©ĹÝ––Ńňő ĺŪĶų≤ť£¨ĹęÕ≥ľ∆ żĺ›Ľś÷∆≥…»ÁŌ¬ŃĹ∑ý≤ĽÕÍ’ŻĶńÕ≥ľ∆Õľ£ģ«Žłýĺ›Õ≥ľ∆ÕľŐŠĻ©Ķń–ŇŌĘ£¨Ĺ‚īūŌ¬Ń–ő Ő‚£ļ
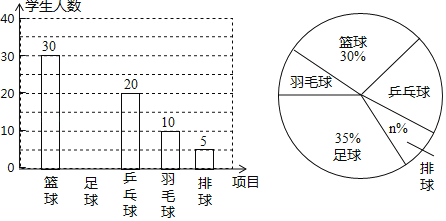
£®1£©m£Ĺ°° °°£¨n£Ĺ°° °°£ģ≤Ę≤Ļ»ęÕľ÷–ĶńŐű–őÕ≥ľ∆Õľ£ģ
£®2£©«Žń„Ļņľ∆ł√–£‘ľ”–∂ŗ…Ŕ√Ż—ß…ķŌ≤įģīÚ∆ĻŇ“«Ú£ģ
£®3£©‘ŕ≥ť≤ťĶńm√Ż—ß…ķ÷–£¨”–A°ĘB°ĘC°ĘDĶ»10√Ż—ß…ķŌ≤Ľ∂”ū√ę«ÚĽÓ∂Į£¨—ß–£īÚň„ī”A°ĘB°ĘC°ĘD’‚4√ŻŇģ…ķ÷–£¨—°»°2√Ż≤őľ”»ę –÷–—ß…ķŇģ◊””ū√ę«ÚĪ»»Ł£¨«Ž”√Ń–ĪŪ∑®ĽÚĽ≠ ų◊īÕľ∑®£¨«ůÕ¨ Ī—°÷–B°ĘCĶńłŇ¬ £ģ
°ĺīūįł°Ņ£®1£©100£¨5£Ľ£®2£©600£Ľ£®3£©![]() .
.
°ĺĹ‚őŲ°Ņ
£®1£©ņļ«Ú30»ň’ľ30%£¨Ņ…Ķ√◊‹»ň ż£¨”…īňŅ…“‘ľ∆ň„≥Ųn£¨«ů≥Ų◊„«Ú»ň ż=100-30-20-10-5=35»ň£¨ľīŅ…Ĺ‚ĺŲő Ő‚£Ľ
£®2£©”√—ýĪĺĻņľ∆◊‹ŐŚĶńňľŌŽľīŅ…Ĺ‚ĺŲő Ő‚£ģ
£®3£©Ľ≠≥Ų ų◊īÕľľīŅ…Ĺ‚ĺŲő Ő‚£ģ
£®1£©”…Ő‚“‚m£Ĺ30°¬30%£Ĺ100£¨ŇŇ«Ú’ľ![]() £Ĺ5%£¨
£Ĺ5%£¨
°ŗn£Ĺ5£¨
◊„«Ú£Ĺ100©Ā30©Ā20©Ā10©Ā5£Ĺ35»ň£¨
Őű–őÕľ»ÁÕľňý ĺ£¨
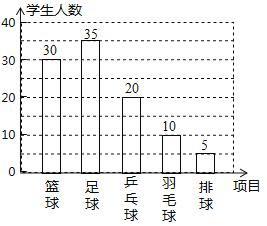
Ļ īūįłő™100£¨5£ģ
£®2£©»Ű»ę–£Ļ≤”–3000√Ż—ß…ķ£¨ł√–£‘ľ”–3000°Ń![]() £Ĺ600√Ż—ß…ķŌ≤įģīÚ∆ĻŇ“«Ú£ģ
£Ĺ600√Ż—ß…ķŌ≤įģīÚ∆ĻŇ“«Ú£ģ
£®3£©Ľ≠ ų◊īÕľĶ√£ļ
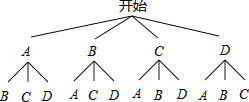
°Ŗ“ĽĻ≤”–12÷÷Ņ…ń‹≥ŲŌ÷ĶńĹŠĻŻ£¨ňŁ√«∂ľ «Ķ»Ņ…ń‹Ķń£¨∑ŻļŌŐűľĢĶń”–ŃĹ÷÷£¨
°ŗÕ¨ Ī—°÷–B°ĘCĶńłŇ¬ ő™![]() £ģ
£ģ



| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°ŅŇ◊őÔŌŖ![]() ”Žx÷ŠĹĽ”ŕA£¨BŃĹĶ„£®OA£ľOB£©£¨”Žy÷ŠĹĽ”ŕĶ„C£ģ
”Žx÷ŠĹĽ”ŕA£¨BŃĹĶ„£®OA£ľOB£©£¨”Žy÷ŠĹĽ”ŕĶ„C£ģ
£®1£©«ůĶ„A£¨B£¨CĶń◊ÝĪÍ£Ľ
£®2£©Ķ„Pī”Ķ„O≥Ų∑Ę£¨“‘√Ņ√Ž2łŲĶ•őĽ≥§∂»ĶńňŔ∂»ŌÚĶ„B‘ň∂Į£¨Õ¨ ĪĶ„E“≤ī”Ķ„O≥Ų∑Ę£¨“‘√Ņ√Ž1łŲĶ•őĽ≥§∂»ĶńňŔ∂»ŌÚĶ„C‘ň∂Į£¨…ŤĶ„PĶń‘ň∂Į Īľšő™t√Ž£®0£ľt£ľ2£©£ģ
ĘŔĻżĶ„E◊ųx÷ŠĶń∆Ĺ––ŌŖ£¨”ŽBCŌŗĹĽ”ŕĶ„D£®»ÁÕľňý ĺ£©£¨ĶĪtő™ļő÷Ķ Ī£¨![]() Ķń÷Ķ◊Ó–°£¨«ů≥Ų’‚łŲ◊Ó–°÷Ķ≤Ę–ī≥Ųīň ĪĶ„E£¨PĶń◊ÝĪÍ£Ľ
Ķń÷Ķ◊Ó–°£¨«ů≥Ų’‚łŲ◊Ó–°÷Ķ≤Ę–ī≥Ųīň ĪĶ„E£¨PĶń◊ÝĪÍ£Ľ
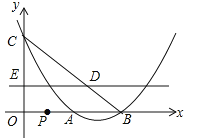
Ęŕ‘ŕ¬ķ◊„ĘŔĶńŐűľĢŌ¬£¨Ň◊őÔŌŖĶń∂‘≥∆÷Š…Ō «∑Ůīś‘ŕĶ„F£¨ Ļ°ųEFPő™÷ĪĹ«»żĹ«–ő£Ņ»Űīś‘ŕ£¨«Ž÷ĪĹ”–ī≥ŲĶ„FĶń◊ÝĪÍ£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”…£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
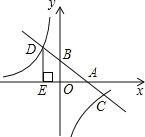
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ÷–£¨“ĽīőļĮ ży=kx+bĶńÕľŌů”Žx÷Š°Ęy÷ŠĹĽ”ŕA°ĘBŃĹĶ„£¨ĹĽ∑īĪ»ņżļĮ ż”ŕC°ĘDŃĹĶ„£¨DE°Õx÷Š”ŕĶ„E£¨“—÷™CĶ„Ķń◊ÝĪÍ «(6£¨-1)£¨DE=3£ģ
(1)«ů∑īĪ»ņżļĮ ż”Ž“ĽīőļĮ żĶńĹ‚őŲ Ĺ
(2)łýĺ›ÕľŌů÷ĪĹ”Ľōīū£ļĶĪxő™ļő÷Ķ Ī£¨“ĽīőļĮ żĶń÷Ķīů”ŕ∑īĪ»ņżļĮ żĶń÷Ķ£ģ
(3)«ů°ųOADĶń√śĽżS°ųOAD£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľňý ĺ£¨Ķ»ĪŖ°ųABC÷–DĶ„ő™ABĪŖ…Ō“Ľ∂ĮĶ„£¨Eő™÷ĪŌŖAC…Ō“ĽĶ„£¨Ĺę°ųADE—ō◊ŇDE’ŘĶĢ£¨Ķ„A¬š‘ŕ÷ĪŌŖBC…Ō£¨∂‘”¶Ķ„ő™F£¨»ŰAB£Ĺ4£¨BF£ļFC£Ĺ1£ļ3£¨‘ÚŌŖ∂őAEĶń≥§∂»ő™_____£ģ

≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľňý ĺ£¨Ń‚–őABCDőĽ”ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ÷–£¨Ň◊őÔŌŖy£Ĺax2+bx+cĺ≠ĻżŃ‚–őĶń»żłŲ∂•Ķ„A°ĘB°ĘC£¨“—÷™A£®©Ā3£¨0£©°ĘB£®0£¨©Ā4£©£ģ
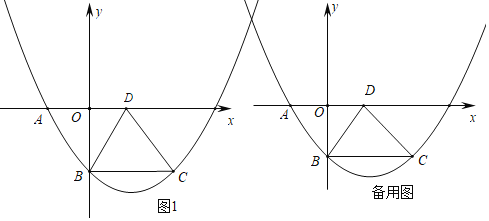
£®1£©«ůŇ◊őÔŌŖĹ‚őŲ Ĺ£Ľ
£®2£©ŌŖ∂őBD…Ō”–“Ľ∂ĮĶ„E£¨ĻżĶ„E◊ųy÷ŠĶń∆Ĺ––ŌŖ£¨ĹĽBC”ŕĶ„F£¨»ŰS°ųBOD£Ĺ4S°ųEBF£¨«ůĶ„EĶń◊ÝĪÍ£Ľ
£®3£©Ň◊őÔŌŖĶń∂‘≥∆÷Š…Ō «∑Ůīś‘ŕĶ„P£¨ Ļ°ųBPD «“‘BDő™–ĪĪŖĶń÷ĪĹ«»żĹ«–ő£Ņ»ÁĻŻīś‘ŕ£¨«ů≥ŲĶ„PĶń◊ÝĪÍ£Ľ»ÁĻŻ≤Ľīś‘ŕ£¨ňĶ√ųņŪ”…£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
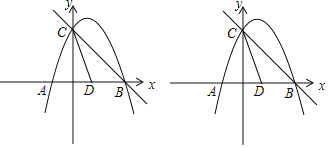
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨Ň◊őÔŌŖy£Ĺ©Āx2+mx+n”Žx÷ŠĹĽ”ŕA£¨BŃĹĶ„£¨y”Ž÷ŠĹĽ”ŕĶ„C£¨Ň◊őÔŌŖĶń∂‘≥∆÷ŠĹĽx÷Š”ŕĶ„D£ģ“—÷™A£®©Ā1£¨0£©£¨C£®0£¨3£©
£®1£©«ůŇ◊őÔŌŖĶńĹ‚őŲ Ĺ£Ľ
£®2£©‘ŕŇ◊őÔŌŖĶń∂‘≥∆÷Š…Ō «∑Ůīś‘ŕPĶ„£¨ Ļ°ųPCD «“‘CDő™—ŁĶńĶ»—Ł»żĹ«–ő£Ņ»ÁĻŻīś‘ŕ£¨÷ĪĹ”–ī≥ŲĶ„PĶń◊ÝĪÍ£Ľ»ÁĻŻ≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”…£Ľ
£®3£©‘ŕBC…Ō∑ĹĶńŇ◊őÔŌŖ…Ō£¨ «∑Ůīś‘ŕĶ„E£¨ ĻĶ√°ųBCEĶń√śĽż◊Óīů£Ņ»Űīś‘ŕ£¨«ů≥ŲĶ„EĶń◊ÝĪÍļÕ°ųBCEĶń√śĽż◊Óīů÷Ķ£Ľ»Ű≤Ľīś‘ŕ£¨ňĶ√ųņŪ”…£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ‘ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ÷–B£®©Ā1£¨0£©£¨A£®0£¨m£©£¨m£ĺ0£¨ĹęŌŖ∂őABŌŖ»∆BĶ„ńś Ī’Ž–ż◊™90°„Ķ√BC£¨ACĶń÷–Ķ„ő™DĶ„£ģ
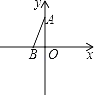
£®1£©m£Ĺ2 Ī£¨Ľ≠Õľ≤Ę÷ĪĹ”–ī≥ŲDĶ„Ķń◊ÝĪÍ°° °°£Ľ
£®2£©»Űňę«ķŌŖ![]() £®x£ľ0£©ĻżC£¨DŃĹĶ„£¨«ů∑īĪ»ņżĶńĹ‚őŲ Ĺ£Ľ
£®x£ľ0£©ĻżC£¨DŃĹĶ„£¨«ů∑īĪ»ņżĶńĹ‚őŲ Ĺ£Ľ
£®3£©‘ŕ£®2£©ĶńŐűľĢŌ¬£¨Ķ„P‘ŕCĶ„◊ů≤ŗ£¨«“‘ŕňę«ķŌŖ…Ō£¨“‘CPő™ĪŖ≥§Ľ≠’ż∑Ĺ–őCPEF£¨«“Ķ„E‘ŕx÷Š…Ō£¨«ůPĶ„◊ÝĪÍ£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨ĺō–őABCDĶńĪŖ≥§AD£Ĺ6£¨AB£Ĺ4£¨Eő™ABĶń÷–Ķ„£¨F‘ŕĪŖBC…Ō£¨«“BF£Ĺ2FC£¨AF∑÷Īū”ŽDE°ĘDBŌŗĹĽ”ŕĶ„M°ĘN£¨‘ÚMNĶń≥§ő™_____£ģ
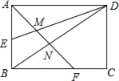
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ∆ů“ĶĶńőŘňģī¶ņŪ”–ŃĹ÷÷∑Ĺ Ĺ£¨“Ľ÷÷ « šňÕĶĹőŘňģ≥ßĹÝ––ľĮ÷–ī¶ņŪ£¨ŃŪ“Ľ÷÷ «Õ®Ļż∆ů“ĶĶń◊‘…Ū…ŤĪłĹÝ––ī¶ņŪ£ģń≥∆ů“Ķ»•ńÍ√Ņ‘¬ĶńőŘňģŃŅĺýő™12000∂÷£¨”…”ŕőŘňģ≥ßī¶”ŕĶų ‘Ĺ◊∂ő£¨őŘňģī¶ņŪń‹Ń¶”–Ōř£¨ł√∆ů“ĶÕ∂◊ ◊‘Ĺ®…ŤĪłī¶ņŪőŘňģ£¨ŃĹ÷÷ī¶ņŪ∑Ĺ ĹÕ¨ ĪĹÝ––£ģ1÷Ń6‘¬£¨ł√∆ů“ĶŌÚőŘňģ≥ß šňÕĶńőŘňģŃŅy1£®∂÷£©”Ž‘¬∑›x£®1°‹x°‹6£¨«“x»°’Ż ż£©÷ģľš¬ķ◊„ĶńļĮ żĻōŌĶ»ÁŌ¬ĪŪ£ļ
‘¬∑›x£®‘¬£© | 1 | 2 | 3 | 4 | 5 | 6 |
šňÕĶńőŘňģŃŅy1£®∂÷£© | 12000 | 6000 | 4000 | 3000 | 2400 | 2000 |
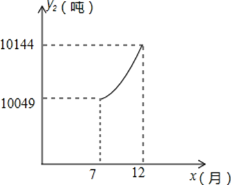
7÷Ń12‘¬£¨ł√∆ů“Ķ◊‘…Ūī¶ņŪĶńőŘňģŃŅy2£®∂÷£©”Ž‘¬∑›x£®7°‹x°‹12£¨«“x»°’Ż ż£©÷ģľš¬ķ◊„∂ĢīőļĮ żĻōŌĶ Ĺő™![]() £®a°Ŕ0£©£ģ∆šÕľŌů»ÁÕľňý ĺ£ģ1÷Ń6‘¬£¨őŘňģ≥ßī¶ņŪ√Ņ∂÷őŘňģĶń∑—”√£ļz1£®‘™£©”Ž‘¬∑›x÷ģľš¬ķ◊„ļĮ żĻōŌĶ Ĺ£ļ
£®a°Ŕ0£©£ģ∆šÕľŌů»ÁÕľňý ĺ£ģ1÷Ń6‘¬£¨őŘňģ≥ßī¶ņŪ√Ņ∂÷őŘňģĶń∑—”√£ļz1£®‘™£©”Ž‘¬∑›x÷ģľš¬ķ◊„ļĮ żĻōŌĶ Ĺ£ļ![]() £¨ł√∆ů“Ķ◊‘…Ūī¶ņŪ√Ņ∂÷őŘňģĶń∑—”√£ļz2£®‘™£©”Ž‘¬∑›x÷ģľš¬ķ◊„ļĮ żĻōŌĶ Ĺ£ļ
£¨ł√∆ů“Ķ◊‘…Ūī¶ņŪ√Ņ∂÷őŘňģĶń∑—”√£ļz2£®‘™£©”Ž‘¬∑›x÷ģľš¬ķ◊„ļĮ żĻōŌĶ Ĺ£ļ![]() £Ľ7÷Ń12‘¬£¨őŘňģ≥ßī¶ņŪ√Ņ∂÷őŘňģĶń∑—”√ĺýő™2‘™£¨ł√∆ů“Ķ◊‘…Ūī¶ņŪ√Ņ∂÷őŘňģĶń∑—”√ĺýő™1.5‘™£ģ
£Ľ7÷Ń12‘¬£¨őŘňģ≥ßī¶ņŪ√Ņ∂÷őŘňģĶń∑—”√ĺýő™2‘™£¨ł√∆ů“Ķ◊‘…Ūī¶ņŪ√Ņ∂÷őŘňģĶń∑—”√ĺýő™1.5‘™£ģ
£®1£©«ŽĻŘ≤žŐ‚÷–ĶńĪŪłŮļÕÕľŌů£¨”√ňý—ßĻżĶń“ĽīőļĮ ż°Ę∑īĪ»ņżļĮ żĽÚ∂ĢīőļĮ żĶń”–Ļō÷™ ∂£¨∑÷Īū÷ĪĹ”–ī≥Ųy1£¨y2”Žx÷ģľšĶńļĮ żĻōŌĶ Ĺ£Ľ
£®2£©«Žń„«ů≥Ųł√∆ů“Ķ»•ńÍńńłŲ‘¬”√”ŕőŘňģī¶ņŪĶń∑—”√W£®‘™£©◊Ó∂ŗ£¨≤Ę«ů≥Ų’‚łŲ◊Ó∂ŗ∑—”√£Ľ
£®3£©ĹŮńÍ“‘ņī£¨”…”ŕ◊‘Ĺ®őŘňģī¶ņŪ…ŤĪłĶń»ę√ś‘ň––£¨ł√∆ů“ĶĺŲ∂®ņ©īů≤ķń‹≤ĘĹęňý”–őŘňģ»ę≤Ņ◊‘…Ūī¶ņŪ£¨Ļņľ∆ņ©īů≤ķń‹ļůĹŮńÍ√Ņ‘¬ĶńőŘňģŃŅ∂ľĹę‘໕ńÍ√Ņ‘¬ĶńĽýī°…Ō‘Ųľ”a%£¨Õ¨ Ī√Ņ∂÷őŘňģī¶ņŪĶń∑—”√Ĺę‘໕ńÍ12‘¬∑›ĶńĽýī°…Ō‘Ųľ”£®a-30£©%£¨ő™ĻńņÝĹŕń‹ĹĶļń£¨ľű«Š∆ů“ĶłļĶ££¨≤∆’Ģ∂‘∆ů“Ķī¶ņŪőŘňģĶń∑—”√ĹÝ––50%Ķń≤Ļ÷ķ£ģ»Űł√∆ů“Ķ√Ņ‘¬ĶńőŘňģī¶ņŪ∑—”√ő™18000‘™£¨«Žľ∆ň„≥ŲaĶń’Ż ż÷Ķ£ģ
£®≤őŅľ żĺ›£ļ![]() °÷15.2£¨
°÷15.2£¨![]() °÷20.5£¨
°÷20.5£¨![]() °÷28.4£©
°÷28.4£©
≤ťŅīīūįłļÕĹ‚őŲ>>
Ļķľ —ß–£”Ň—° - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com