
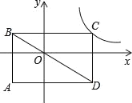
【题目】在平面直角坐标系中B(﹣1,0),A(0,m),m>0,将线段AB线绕B点逆时针旋转90°得BC,AC的中点为D点.
(1)m=2时,画图并直接写出D点的坐标 ;
(2)若双曲线![]() (x<0)过C,D两点,求反比例的解析式;
(x<0)过C,D两点,求反比例的解析式;
(3)在(2)的条件下,点P在C点左侧,且在双曲线上,以CP为边长画正方形CPEF,且点E在x轴上,求P点坐标.
【答案】(1)见解析,![]() ;(2)
;(2)![]() ;(3)见解析,点P坐标为(﹣2﹣2
;(3)见解析,点P坐标为(﹣2﹣2![]() ,2
,2![]() ﹣2)
﹣2)
【解析】
(1)过点C作CM⊥x轴,由旋转的性质可得AB=BC,∠ABC=90°,由“AAS”可证△ABO≌△BCM,可得AO=BM=m,BO=CM=1,可得点C坐标,由中点坐标公式可求点D坐标;
(2)先求点C,点D坐标,代入解析式可求反比例函数的解析式;
(3)过点P作PQ⊥BE,过点C作CD⊥PQ,由“AAS”可证△CDP≌△PQE,可得PD=EQ,CD=PQ,由点P(x,y)(x<0),点C坐标(4,1),可得y=4x,由反比例函数的性质可得xy=4,可求x,y的值,即可求P点坐标.
解:(1)过点C作CM⊥x轴,
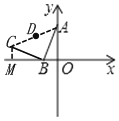
∵将线段AB线绕B点逆时针旋转90°
∴AB=BC,∠ABC=90°
∴∠ABO+∠CBM=90°
∵∠AOB=90°,
∴∠ABO+∠BAO=90°
∴∠CBM=∠BAO,且BC=AB,∠CMB=∠AOB=90°
∴△ABO≌△BCM(AAS)
∴AO=BM=m,BO=CM=1
∵m=2
∴MO=3,
∴点C(﹣3,1),且点A(0,2),AC的中点为D点.
∴点D坐标为(![]() ),
),
故答案为:(![]() );
);
(2)由(1)可得:AO=BM=m,BO=CM=1
∴MO=1+m,
∴点C(﹣1﹣m,1),且点A(0,m),AC的中点为D点.
∴点D坐标(![]() )
)
∵双曲线y=![]() (x<0)过C,D两点,
(x<0)过C,D两点,
∴1×(﹣1﹣m)=![]()
∴m=3,点C坐标(﹣4,1)
∴k=﹣4,
∴双曲线解析式:![]() ;
;
(3)如图,过点P作PQ⊥BE,过点C作CD⊥PQ,
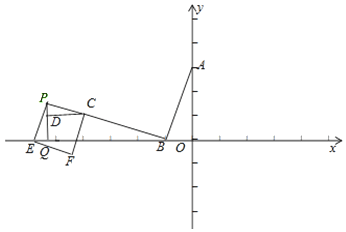
设点P(x,y)(x<0)
∵四边形CPEF是正方形,
∴CP=PE,
∵PQ⊥BE,CD⊥PQ,
∴∠PEB+∠EPQ=90°,∠EPQ+∠CPQ=90°
∴∠CPQ=∠PEB,且PC=PE,∠CDP=∠PQE=90°
∴△CDP≌△PQE(AAS)
∴PD=EQ,CD=PQ,
∵点P(x,y)(x<0),点C坐标(﹣4,1)
∴CD=﹣4﹣x=PQ,PD=y﹣1=EQ,PQ=y,BQ=﹣x,
∴y=﹣4﹣x,
∵点P在C点左侧,且在双曲线上,
∴xy=﹣4
∴x(﹣4﹣x)=﹣4
∴x1=![]() ,x2=
,x2=![]() (不合题意),
(不合题意),
∴y=﹣4﹣x=![]()
∴点P坐标为(![]() ,
,![]() ).
).


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】为了提高学生的身体素质,某班级决定开展球类活动,要求每个学生必须在篮球、足球、排球、乒乓球、羽毛球中选择一项参加训练(只选择一项),根据学生的报名情况制成如下统计表:
项目 | 篮球 | 足球 | 排球 | 乒乓球 | 羽毛球 |
报名人数 | 12 | 8 | 4 | a | 10 |
占总人数的百分比 | 24% | b |
(1)该班学生的总人数为 人;
(2)由表中的数据可知:a= ,b= ;
(3)报名参加排球训练的四个人为两男(分别记为A、B)两女(分别记为C、D),现要随机在这4人中选2人参加学校组织的校级训练,请用列表或树状图的方法求出刚好选中一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装公司招工广告承诺:熟练工人每月工资至少3000元.每天工作8小时,一个月工作25天.月工资底薪800元,另加计件工资.加工1件A型服装计酬16元,加工1件B型服装计酬12元.在工作中发现一名熟练工加工1件A型服装和2件B型服装需4小时,加工3件A型服装和1件B型服装需7小时.(工人月工资=底薪+计件工资)
(1)一名熟练工加工1件A型服装和1件B型服装各需要多少小时?
(2)一段时间后,公司规定:“每名工人每月必须加工A,B两种型号的服装,且加工A型服装数量不少于B型服装的一半”.设一名熟练工人每月加工A型服装a件,工资总额为W元.请你运用所学知识判断该公司在执行规定后是否违背了广告承诺?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解全校3000名学生对学校设置的足球、篮球、乒乓球、羽毛球、排球共五项球类活动的喜爱情况,在全校范围内随机调查了m名学生(每名学生必选且只能选择这五项活动中的一种)进行了问卷调查,将统计数据绘制成如下两幅不完整的统计图.请根据统计图提供的信息,解答下列问题:
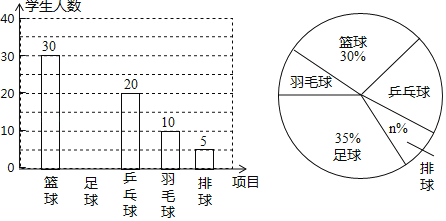
(1)m= ,n= .并补全图中的条形统计图.
(2)请你估计该校约有多少名学生喜爱打乒乓球.
(3)在抽查的m名学生中,有A、B、C、D等10名学生喜欢羽毛球活动,学校打算从A、B、C、D这4名女生中,选取2名参加全市中学生女子羽毛球比赛,请用列表法或画树状图法,求同时选中B、C的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“优秀传统文化进校园”活动中,学校计划每周二下午第三节课时间开展此项活动,拟开展活动项目为:剪纸,武术,书法,器乐,要求七年级学生人人参加,并且每人只能参加其中一项活动.教务处在该校七年级学生中随机抽取了100名学生进行调查,并对此进行统计,绘制了如图所示的条形统计图和扇形统计图(均不完整).

请解答下列问题:
(1)请补全条形统计图和扇形统计图;
(2)在参加“剪纸”活动项目的学生中,男生所占的百分比是多少?
(3)若该校七年级学生共有500人,请估计其中参加“书法”项目活动的有多少人?
(4)学校教务处要从这些被调查的女生中,随机抽取一人了解具体情况,那么正好抽到参加“器乐”活动项目的女生的概率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数![]() 的图象上.若点A的坐标为(﹣4,﹣4),则k的值为( )
的图象上.若点A的坐标为(﹣4,﹣4),则k的值为( )
A. 16B. ﹣3C. 5D. 5或﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=kx+b(k<0),经过点(6,0),且与坐标轴围成的三角形的面积是9,与函数y=![]() (x>0)的图象G交于A,B两点.
(x>0)的图象G交于A,B两点.
(1)求直线的表达式;
(2)横、纵坐标都是整数的点叫作整点.记图象G在点A、B之间的部分与线段AB围成的区域(不含边界)为W.
①当m=2时,直接写出区域W内的整点的坐标 ;
②若区域W内恰有3个整数点,结合函数图象,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“高低杠”是女子体操特有的一个竞技项目,其比赛器材由高、低两根平行杠及若干支架组成,运动员可根据自己的身高和习惯在规定范围内调节高、低两杠间的距离.某兴趣小组根据高低杠器材的一种截面图编制了如下数学问题,请你解答.
如图所示,底座上A,B两点间的距离为90cm.低杠上点C到直线AB的距离CE的长为155cm,高杠上点D到直线AB的距离DF的长为234cm,已知低杠的支架AC与直线AB的夹角∠CAE为82.4°,高杠的支架BD与直线AB的夹角∠DBF为80.3°.求高、低杠间的水平距离CH的长.(结果精确到1cm,参考数据sin82.4°≈0.991,cos82.4°≈0.132,tan82.4°≈7.500,sin80.3°≈0.983,cos80.3°≈0.168,tan80.3°≈5.850)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com