
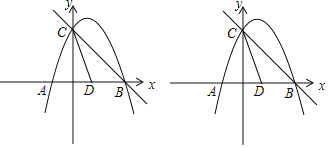
【题目】如图,抛物线y=﹣x2+mx+n与x轴交于A,B两点,y与轴交于点C,抛物线的对称轴交x轴于点D.已知A(﹣1,0),C(0,3)
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在P点,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出点P的坐标;如果不存在,请说明理由;
(3)在BC上方的抛物线上,是否存在点E,使得△BCE的面积最大?若存在,求出点E的坐标和△BCE的面积最大值;若不存在,说明理由.
【答案】(1)y=﹣x2+2x+3;(2)点P的坐标有四个,分别是(1,0)或(1,6)或(1,![]() )或(1,﹣
)或(1,﹣![]() );(3)△BCE的面积最大为
);(3)△BCE的面积最大为![]() ,此时E(
,此时E(![]() ,
,![]() ).
).
【解析】
(1)把A、C两点的坐标代入y=-x2+mx+n,利用待定系数法即可求出二次函数的解析式;
(2)当△PCD是以CD为腰的等腰三角形时,可分两种情况讨论:①PC=CD;②PD=CD.设出点P的坐标,利用两点间的距离公式列出方程求解即可;
(3)设E(x,-x2+2x+3),过E作EF∥y轴,交直线BC于点F,交x轴于N,过C作CM⊥EF于M,根据S△BCE=S△CEF+S△BEF即可得出△BCE的面积关于x的函数关系式,进而求得E的坐标和△BCE的面积最大值.
(1)把A(﹣1,0),C(0,3)代入y=﹣x2+mx+n,
得:![]() ,解得:
,解得:![]() ,
,
∴抛物线的解析式为:y=﹣x2+2x+3;
(2)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴对称轴为直线x=1,
∴D(1,0).
设点P的坐标为(1,t),
∵C(0,3),
∴CD2=12+32=10.
当△PCD是以CD为腰的等腰三角形时,可分两种情况讨论:
①若PC=CD,则12+(t﹣3)2=10,解得t=0或6,
所以点P的坐标为(1,0)或(1,6);
②若PD=CD,则t2=10,解得t=±![]() ,
,
所以点P的坐标为(1,![]() )或(1,﹣
)或(1,﹣![]() );
);
综上所述,点P的坐标有四个,分别是(1,0)或(1,6)或(1,![]() )或(1,﹣
)或(1,﹣![]() );
);
(3)当y=0时,﹣x2+2x+3=0,
解得:x1=﹣1,x2=3,
∴B(3,0),
设直线BC的解析式为:y=kx+b,
把B(3,0)、C(0,3)代入得:![]() ,
,
解得:![]() ,
,
∴直线BC的解析式为:y=﹣x+3.
如图,过E作EF∥y轴,交直线BC于点F,交x轴于N,过C作CM⊥EF于M,
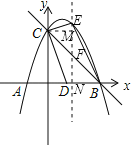
设E(x,﹣x2+2x+3),则F(x,﹣x+3),
∴EF=(﹣x2+2x+3)﹣(﹣x+3)=﹣x2+3x(0<x<3),
∵S△BCE=S△CEF+S△BEF
=![]() EFCM+
EFCM+![]() EFBN
EFBN
=![]() EF(CM+BN)
EF(CM+BN)
=![]() EFOB
EFOB
=![]() ×3(﹣x2+3x)
×3(﹣x2+3x)
=![]()
=![]() ,
,
∴当x=![]() 时,△BCE的面积最大为
时,△BCE的面积最大为![]() ,此时E(
,此时E(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
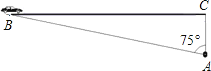
【题目】超速行驶是引发交通事故的主要原因之一.上周末,小明和三位同学尝试用自己所学的知识检测车速.如图,观测点设在A处,离益阳大道的距离(AC)为30米.这时,一辆小轿车由西向东匀速行驶,测得此车从B处行驶到C处所用的时间为8秒,∠BAC=75°.
(1)求B、C两点的距离;
(2)请判断此车是否超过了益阳大道60千米/小时的限制速度?
(计算时距离精确到1米,参考数据:sin75°≈0.9659,cos75°≈0.2588,tan75°≈3.732,![]() ,60千米/小时≈16.7米/秒)
,60千米/小时≈16.7米/秒)
查看答案和解析>>
科目:初中数学 来源: 题型:
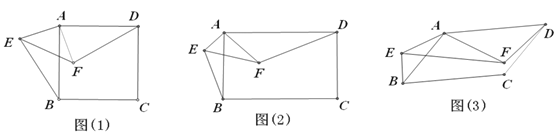
【题目】如图所示,(1)正方形ABCD及等腰Rt△AEF有公共顶点A,∠EAF=90°, 连接BE、DF.将Rt△AEF绕点A旋转,在旋转过程中,BE、DF具有怎样的数量关系和位置关系?结合图(1)给予证明;
(2)将(1)中的正方形ABCD变为矩形ABCD,等腰Rt△AEF变为Rt△AEF,且AD=kAB,AF=kAE,其他条件不变.(1)中的结论是否发生变化?结合图(2)说明理由;
(3)将(2)中的矩形ABCD变为平行四边形ABCD,将Rt△AEF变为△AEF,且∠BAD=∠EAF=![]() ,其他条件不变.(2)中的结论是否发生变化?结合图(3),如果不变,直接写出结论;如果变化,直接用k表示出线段BE、DF的数量关系,用
,其他条件不变.(2)中的结论是否发生变化?结合图(3),如果不变,直接写出结论;如果变化,直接用k表示出线段BE、DF的数量关系,用![]() 表示出直线BE、DF形成的锐角
表示出直线BE、DF形成的锐角![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王从同事小李手中接收一批生产任务,派单方要求必须在15天内完成,届时承以每件60元的价格全部回收,小王在接受任务之后,其生产的任务y(件)与生产的天数x(天)关系如图1所示,其中在生产6天之后,每天的生产数量达到了30件.
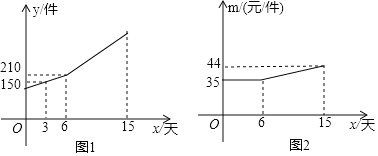
(1)求y与x之间的函数表达式;
(2)设第x天生产的产品成本为m元/件,m与x的函数图象如图2所示,若小王第x天的利润为W元,求W与x的关系式,并求出第几天后小王的利润可达到最大值,最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解全校3000名学生对学校设置的足球、篮球、乒乓球、羽毛球、排球共五项球类活动的喜爱情况,在全校范围内随机调查了m名学生(每名学生必选且只能选择这五项活动中的一种)进行了问卷调查,将统计数据绘制成如下两幅不完整的统计图.请根据统计图提供的信息,解答下列问题:
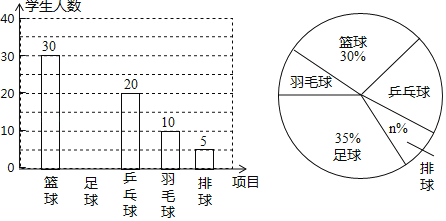
(1)m= ,n= .并补全图中的条形统计图.
(2)请你估计该校约有多少名学生喜爱打乒乓球.
(3)在抽查的m名学生中,有A、B、C、D等10名学生喜欢羽毛球活动,学校打算从A、B、C、D这4名女生中,选取2名参加全市中学生女子羽毛球比赛,请用列表法或画树状图法,求同时选中B、C的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有A,B两种商品,买2件A商品和1件B商品用了90元,买3件A商品和2件B商品共用了160元.
(1)求A,B两种商品每件多少元?
(2)如果小亮准备购买A,B两种商品共10件,总费用不超过350元,且不低于300元,问有几种购买方案,哪种方案费用最低?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“优秀传统文化进校园”活动中,学校计划每周二下午第三节课时间开展此项活动,拟开展活动项目为:剪纸,武术,书法,器乐,要求七年级学生人人参加,并且每人只能参加其中一项活动.教务处在该校七年级学生中随机抽取了100名学生进行调查,并对此进行统计,绘制了如图所示的条形统计图和扇形统计图(均不完整).

请解答下列问题:
(1)请补全条形统计图和扇形统计图;
(2)在参加“剪纸”活动项目的学生中,男生所占的百分比是多少?
(3)若该校七年级学生共有500人,请估计其中参加“书法”项目活动的有多少人?
(4)学校教务处要从这些被调查的女生中,随机抽取一人了解具体情况,那么正好抽到参加“器乐”活动项目的女生的概率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
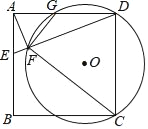
【题目】如图,在正方形ABCD中,E是AB上一点,连接DE.过点A作AF⊥DE,垂足为F,⊙O经过点C、D、F,与AD相交于点G.
(1)求证:△AFG∽△DFC;
(2)若正方形ABCD的边长为4,AE=1,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】爸爸想送小明一个书包和一辆自行车作为新年礼物,在甲、乙两商场都发现同款的自行车单价相同,书包单价也相同,自行车和书包单价之和为452元,且自行车的单价比书包的单价4倍少8元.
(1)求自行车和书包单价各为多少元;
(2)新年来临赶上商家促销,乙商场所有商品打八五折(即8.5折)销售,甲全场购物毎满100元返购物券30元(即不足100元不返券,满100元送30元购物券,满200元送60元购物券),并可当场用于购物,购物券全场通用.但爸爸只带了400元钱,如果他只在同一家商场购买看中的两样物品,在哪一家买更省钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com