
ЁОЬтФПЁПШчЭМЫљЪОЃЌЃЈ1ЃЉе§ЗНаЮABCDМАЕШбќRtЁїAEFгаЙЋЙВЖЅЕуA,ЁЯEAFЃН90Ёу, СЌНгBEЁЂDF.НЋRtЁїAEFШЦЕуAа§зЊ,дка§зЊЙ§ГЬжаЃЌBEЁЂDFОпгадѕбљЕФЪ§СПЙиЯЕКЭЮЛжУЙиЯЕЃПНсКЯЭМ(1)ИјгшжЄУїЃЛ
(2)НЋЃЈ1ЃЉжаЕФе§ЗНаЮABCDБфЮЊОиаЮABCDЃЌЕШбќRtЁїAEFБфЮЊRtЁїAEFЃЌЧвADЃНkAB,AFЃНkAE,ЦфЫћЬѕМўВЛБф.(1)жаЕФНсТлЪЧЗёЗЂЩњБфЛЏЃПНсКЯЭМ(2)ЫЕУїРэгЩЃЛ
(3)НЋЃЈ2ЃЉжаЕФОиаЮABCDБфЮЊЦНааЫФБпаЮABCDЃЌНЋRtЁїAEFБфЮЊЁїAEFЃЌЧвЁЯBADЃНЁЯEAFЃН![]() ЃЌЦфЫћЬѕМўВЛБф.(2)жаЕФНсТлЪЧЗёЗЂЩњБфЛЏЃПНсКЯЭМ(3)ЃЌШчЙћВЛБфЃЌжБНгаДГіНсТлЃЛШчЙћБфЛЏЃЌжБНггУkБэЪОГіЯпЖЮBEЁЂDFЕФЪ§СПЙиЯЕЃЌгУ
ЃЌЦфЫћЬѕМўВЛБф.(2)жаЕФНсТлЪЧЗёЗЂЩњБфЛЏЃПНсКЯЭМ(3)ЃЌШчЙћВЛБфЃЌжБНгаДГіНсТлЃЛШчЙћБфЛЏЃЌжБНггУkБэЪОГіЯпЖЮBEЁЂDFЕФЪ§СПЙиЯЕЃЌгУ![]() БэЪОГіжБЯпBEЁЂDFаЮГЩЕФШёНЧ
БэЪОГіжБЯпBEЁЂDFаЮГЩЕФШёНЧ![]() .
.
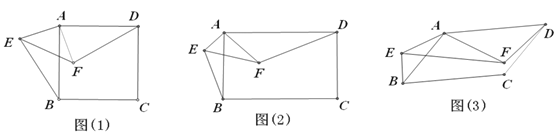
ЁОД№АИЁПЃЈ1ЃЉDF=BEЧвDFЁЭBEЃЌжЄУїМћНтЮіЃЛЃЈ2ЃЉЪ§СПЙиЯЕИФБфЃЌЮЛжУЙиЯЕВЛБфЃЌМДDF=kBEЃЌDFЁЭBEЃЛЃЈ3ЃЉВЛИФБфЃЎDF=kBEЃЌІТ=180Ёу-ІС
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉИљОна§зЊЕФЙ§ГЬжаЯпЖЮЕФГЄЖШВЛБфЃЌЕУЕНAF=AEЃЌгжЁЯBAEгыЁЯDAFЖМгыЁЯBAFЛЅгрЃЌЫљвдЁЯBA E=ЁЯDAFЃЌЫљвдЁїFADЁеЁїEABЃЌвђДЫBEгыDFЯрЕШЃЌбгГЄDFНЛBEгкGЃЌИљОнШЋЕШШ§НЧаЮЕФЖдгІНЧЯрЕШКЭЫФБпаЮЕФФкНЧКЭЕШгк360ЁуЧѓГіЁЯEGF=90ЁуЃЌЫљвдDFЁЭBEЃЛЃЈ2ЃЉЕШЭЌЃЈ1ЃЉЕФЗНЗЈЃЌвђЮЊОиаЮЕФСкБпВЛЯрЕШЃЌЕЋИљОнЬтвтЃЌПЩвдЕУЕНЖдгІБпГЩБШР§ЃЌЫљвдЁїFADЁзЁїEABЃЌЫљвдDF=kBEЃЌЭЌРэЃЌИљОнЯрЫЦШ§НЧаЮЕФЖдгІНЧЯрЕШКЭЫФБпаЮЕФФкНЧКЭЕШгк360ЁуЧѓГіЁЯEHF=90ЁуЃЌЫљвдDFЁЭBEЃЛ
ЃЈ3ЃЉгыЃЈ2ЃЉЕФжЄУїЗНЗЈЯрЭЌЃЌЕЋИљОнЯрЫЦШ§НЧаЮЕФЖдгІНЧЯрЕШКЭЫФБпаЮЕФФкНЧКЭЕШгк360ЁуЧѓГіЁЯEAF+ЁЯEHF=180ЁуЃЌЫљвдDFгыBEЕФМаНЧІТ=180Ёу-ІСЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉDFгыBEЛЅЯрДЙжБЧвЯрЕШЃЎ
жЄУїЃКбгГЄDFЗжБ№НЛABЁЂBEгкЕуPЁЂG
дке§ЗНаЮABCDКЭЕШбќжБНЧЁїAEFжа
AD=ABЃЌAF=AEЃЌ
ЁЯBAD=ЁЯEAF=90Ёу
ЁрЁЯFAD=ЁЯEAB
ЁрЁїFADЁеЁїEABЃЈ2ЗжЃЉ
ЁрЁЯAFD=ЁЯAEBЃЌDF="BE"
ЁпЁЯAFD+ЁЯAFG=180ЁуЃЌ
ЁрЁЯAEG+ЁЯAFG=180ЁуЃЌ
ЁпЁЯEAF=90ЁуЃЌ
ЁрDFЁЭBE
ЃЈ2ЃЉЪ§СПЙиЯЕИФБфЃЌЮЛжУЙиЯЕВЛБфЃЎDF=kBEЃЌDFЁЭBEЃЎ
бгГЄDFНЛEBгкЕуHЃЌ
ЁпAD=kABЃЌAF="kAE"
Ёр![]() ,
, ![]()
Ёр![]()
ЁпЁЯBAD=ЁЯEAF="a"
ЁрЁЯFAD=ЁЯEAB
ЁрЁїFADЁзЁїEAB
Ёр![]()
ЁрDF="kBE"
ЁпЁїFADЁзЁїEABЃЌ
ЁрЁЯAFD=ЁЯAEBЃЌ
ЁпЁЯAFD+ЁЯAFH=180ЁуЃЌ
ЁрЁЯAEH+ЁЯAFH=180ЁуЃЌ
ЁпЁЯEAF=90ЁуЃЌ
ЁрЁЯEHF=180Ёу-90Ёу=90ЁуЃЌ
ЁрDFЁЭBE


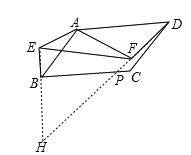
ЃЈ3ЃЉВЛИФБфЃЎDF=kBEЃЌІТ=180Ёу-aЃЎ
бгГЄDFНЛEBЕФбгГЄЯпгкЕуHЃЌ
ЁпAD=kABЃЌAF="kAE"
Ёр![]() ,
, ![]()
Ёр![]()
ЁпЁЯBAD=ЁЯEAF="a"
ЁрЁЯFAD=ЁЯEAB
ЁрЁїFADЁзЁїEAB
Ёр![]()
ЁрDF=kBE
гЩЁїFADЁзЁїEABЕУЁЯAFD=ЁЯAEB
ЁпЁЯAFD+ЁЯAFH=180Ёу
ЁрЁЯAEB+ЁЯAFH=180Ёу
ЁпЫФБпаЮAEHFЕФФкНЧКЭЮЊ360ЁуЃЌ
ЁрЁЯEAF+ЁЯEHF=180Ёу
ЁпЁЯEAF=ІСЃЌЁЯEHF=ІТ
Ёрa+ІТ=180ЁуЁрІТ=180Ёу-a



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
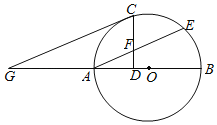
ЁОЬтФПЁПШчЭМЫљЪОЃЌABЪЧЁбOЕФжБОЖЃЌAEЪЧЯвЃЌCЪЧСгЛЁAEЕФжаЕуЃЌЙ§CзїCDЁЭABгкЕуDЃЌCDНЛAEгкЕуFЃЌЙ§CзїCGЁЮAEНЛBAЕФбгГЄЯпгкЕуGЃЎ
ЃЈ1ЃЉЧѓжЄЃКCGЪЧЁбOЕФЧаЯпЃЎ
ЃЈ2ЃЉЧѓжЄЃКAFЃНCFЃЎ
ЃЈ3ЃЉШєsinGЃН0.6ЃЌCFЃН4ЃЌЧѓGAЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
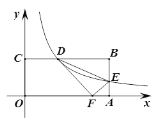
ЁОЬтФПЁПШчЭМЃЌОиаЮOABCЕФБпOAЁЂOCЗжБ№дкxжсЁЂyжсЩЯЃЌЕуB ЕФзјБъЮЊ(8,4)ЃЌЗДБШР§КЏЪ§y=![]() (k>0)ЕФЭМЯѓЗжБ№НЛБпBCЁЂAB гкЕуDЁЂEЃЌСЌНсDEЃЌЁїDEFгыЁїDEBЙигкжБЯпDEЖдГЦЃЌЕБЕуFЧЁКУТфдкЯпЖЮOAЩЯЪБЃЌдђkЕФжЕЪЧ________.
(k>0)ЕФЭМЯѓЗжБ№НЛБпBCЁЂAB гкЕуDЁЂEЃЌСЌНсDEЃЌЁїDEFгыЁїDEBЙигкжБЯпDEЖдГЦЃЌЕБЕуFЧЁКУТфдкЯпЖЮOAЩЯЪБЃЌдђkЕФжЕЪЧ________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
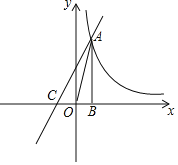
ЁОЬтФПЁПШчЭМЃЌвбжЊЗДБШР§КЏЪ§yЃН![]() ЕФЭМЯѓОЙ§ЕквЛЯѓЯоФкЕФвЛЕуA(nЃЌ4)ЃЌЙ§ЕуAзїABЁЭxжсгкЕуBЃЌЧвЁїAOBЕФУцЛ§ЮЊ2ЃЎ
ЕФЭМЯѓОЙ§ЕквЛЯѓЯоФкЕФвЛЕуA(nЃЌ4)ЃЌЙ§ЕуAзїABЁЭxжсгкЕуBЃЌЧвЁїAOBЕФУцЛ§ЮЊ2ЃЎ
(1)ЧѓmКЭnЕФжЕЃЛ
(2)ШєвЛДЮКЏЪ§yЃНkx+2ЕФЭМЯѓОЙ§ЕуAЃЌВЂЧвгыxжсЯрНЛгкЕуCЃЌЧѓЯпЖЮACЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
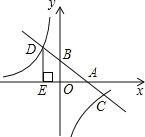
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвЛДЮКЏЪ§y=kx+bЕФЭМЯѓгыxжсЁЂyжсНЛгкAЁЂBСНЕуЃЌНЛЗДБШР§КЏЪ§гкCЁЂDСНЕуЃЌDEЁЭxжсгкЕуEЃЌвбжЊCЕуЕФзјБъЪЧ(6ЃЌ-1)ЃЌDE=3ЃЎ
(1)ЧѓЗДБШР§КЏЪ§гывЛДЮКЏЪ§ЕФНтЮіЪН
(2)ИљОнЭМЯѓжБНгЛиД№ЃКЕБxЮЊКЮжЕЪБЃЌвЛДЮКЏЪ§ЕФжЕДѓгкЗДБШР§КЏЪ§ЕФжЕЃЎ
(3)ЧѓЁїOADЕФУцЛ§SЁїOADЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§yЃНkxЃЋbЕФЭМЯѓгыЗДБШР§КЏЪ§yЃН![]() (xЃО0)ЕФЭМЯѓНЛгкЕуP(nЃЌ2)ЃЌгыxжсНЛгкЕуA(Ѓ4,0)ЃЌгыyжсНЛгкЕуCЃЌPBЁЭxжсгкЕуBЃЌЕуAгыЕуBЙигкyжсЖдГЦЃЎ
(xЃО0)ЕФЭМЯѓНЛгкЕуP(nЃЌ2)ЃЌгыxжсНЛгкЕуA(Ѓ4,0)ЃЌгыyжсНЛгкЕуCЃЌPBЁЭxжсгкЕуBЃЌЕуAгыЕуBЙигкyжсЖдГЦЃЎ
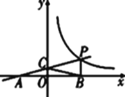
(1)ЧѓвЛДЮКЏЪ§ЁЂЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
(2)ЧѓжЄЃКЕуCЮЊЯпЖЮAPЕФжаЕуЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌЕШБпЁїABCжаDЕуЮЊABБпЩЯвЛЖЏЕуЃЌEЮЊжБЯпACЩЯвЛЕуЃЌНЋЁїADEбизХDEелЕўЃЌЕуAТфдкжБЯпBCЩЯЃЌЖдгІЕуЮЊFЃЌШєABЃН4ЃЌBFЃКFCЃН1ЃК3ЃЌдђЯпЖЮAEЕФГЄЖШЮЊ_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
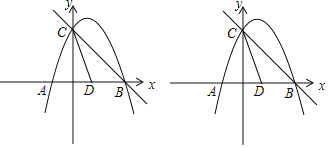
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНЉx2+mx+nгыxжсНЛгкAЃЌBСНЕуЃЌyгыжсНЛгкЕуCЃЌХзЮяЯпЕФЖдГЦжсНЛxжсгкЕуDЃЎвбжЊAЃЈЉ1ЃЌ0ЃЉЃЌCЃЈ0ЃЌ3ЃЉ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉдкХзЮяЯпЕФЖдГЦжсЩЯЪЧЗёДцдкPЕуЃЌЪЙЁїPCDЪЧвдCDЮЊбќЕФЕШбќШ§НЧаЮЃПШчЙћДцдкЃЌжБНгаДГіЕуPЕФзјБъЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉдкBCЩЯЗНЕФХзЮяЯпЩЯЃЌЪЧЗёДцдкЕуEЃЌЪЙЕУЁїBCEЕФУцЛ§зюДѓЃПШєДцдкЃЌЧѓГіЕуEЕФзјБъКЭЁїBCEЕФУцЛ§зюДѓжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮABCDжаЃЌABЃН4ЃЌЕуEЁЂFЗжБ№дкCDЁЂADЩЯЃЌCEЃНDFЃЌBEЁЂCFЯрНЛгкЕуGЃЌШєЭМжавѕгАВПЗжЕФУцЛ§гые§ЗНаЮABCDЕФУцЛ§жЎБШЮЊ3ЃК4ЃЌдђЁїBCGЕФУцЛ§ЮЊ_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com