
【题目】如图1,在平面直角坐标系中,一次函数![]() 的图象与
的图象与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,点
,点![]() ,过点
,过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() ,过点
,过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() ,两条垂线相交于点
,两条垂线相交于点![]() .
.
(1)线段![]() ,
,![]() ,
,![]() 的长分别为
的长分别为![]() _______,
_______,![]() _________,
_________,![]() _________;
_________;
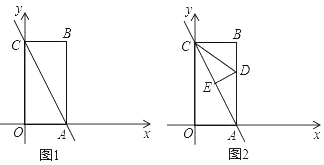
(2)折叠图1中的![]() ,使点
,使点![]() 与点
与点![]() 重合,再将折叠后的图形展开,折痕
重合,再将折叠后的图形展开,折痕![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,如图2.
,如图2.
①求线段![]() 的长;
的长;
②在![]() 轴上,是否存在点
轴上,是否存在点![]() ,使得
,使得![]() 为等腰三角形?若存在,请直接写出符合条件的所有点
为等腰三角形?若存在,请直接写出符合条件的所有点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)8;4;![]() ;(2)①线段AD的长为5;②点P的坐标为(0,3)或(0,-3)或(0,2)或(0,8)或(0,
;(2)①线段AD的长为5;②点P的坐标为(0,3)或(0,-3)或(0,2)或(0,8)或(0,![]() ).
).
【解析】
(1)利用一次函数图象上点的坐标特征可求出点A,C的坐标,利用矩形的性质及勾股定理,可得出AB,BC,AC的长;
(2)①设AD=a,则CD=a,BD=8-a,在Rt△BCD中,利用勾股定理可求出a的值,进而可得出线段AD的长;
②设点P的坐标为(0,t),利用两点间的距离公式可求出AD2,AP2,DP2的值,分AP=AD,AD=DP及AP=DP三种情况,可得出关于t的一元二次方程(或一元一次方程),解之即可得出t的值,进而可得出点P的坐标.
解:(1)如图:

当x=0时,y=-2x+8=8,
∴点C的坐标为(0,8);
当y=0时,-2x+8=0,解得:x=4,
∴点A的坐标为(4,0).
由已知可得:四边形OABC为矩形,
∴AB=OC=8,BC=OA=4,AC=![]() .
.
故答案为:8;4;![]() .
.
(2)①设AD=a,则CD=a,BD=8-a.
在Rt△BCD中,CD2=BC2+BD2,即a2=42+(8-a)2,
解得:a=5,
∴线段AD的长为5.
②存在,如图:

设点P的坐标为(0,t).
∵点A的坐标为(4,0),点D的坐标为(4,5),
∴AD2=25,AP2=(0-4)2+(t-0)2=t2+16,DP2=(0-4)2+(t-5)2=t2-10t+41.
当AP=AD时,t2+16=25,
解得:t=±3,
∴点P的坐标为(0,3)或(0,-3);
当AD=DP时,25=t2-10t+41,
解得:t1=2,t2=8,
∴点P的坐标为(0,2)或(0,8);
当AP=DP时,t2+16=t2-10t+41,
解得:t=![]() ,
,
∴点P的坐标为(0,![]() ).
).
综上所述:在y轴上存在点P,使得△APD为等腰三角形,点P的坐标为(0,3)或(0,-3)或(0,2)或(0,8)或(0,![]() ).
).


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2-2x-3与x轴交于A、B两点,与y轴交于点C.
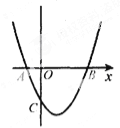
(1)点A的坐标为 点B的坐标为 ,点C的坐标为 ;
(2)设抛物线y=x2-2x-3的顶点坐标为M,求四边形ABMC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
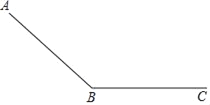
【题目】如图,一个滑道由滑坡(AB段)和缓冲带(BC段)组成,滑雪者在滑坡上滑行的距离y1(单位:m)和滑行时间t1(单位s)满足二次函数关系,并测得相关数据:
滑行时间t1/s | 0 | 1 | 2 | 3 | 4 |
滑行距离y1/s | 0 | 4.5 | 14 | 28.5 | 48 |
滑雪者在缓冲带上滑行的距离y2(单位:m)和滑行时间t2(单位:s)满足:y2=52t2﹣2t22,滑雪者从A出发在缓冲带BC上停止,一共用了23s.
(1)求y1和t1满足的二次函数解析式;
(2)求滑坡AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】再读教材:
宽与长的比是 ![]() (约为0.618)的矩形叫做黄金矩形,黄金矩形给我们以协调,匀称的美感.世界各国许多著名的建筑.为取得最佳的视觉效果,都采用了黄金矩形的设计,下面我们用宽为2的矩形纸片折叠黄金矩形.(提示; MN=2)
(约为0.618)的矩形叫做黄金矩形,黄金矩形给我们以协调,匀称的美感.世界各国许多著名的建筑.为取得最佳的视觉效果,都采用了黄金矩形的设计,下面我们用宽为2的矩形纸片折叠黄金矩形.(提示; MN=2)
第一步,在矩形纸片一端.利用图①的方法折出一个正方形,然后把纸片展平.
第二步,如图②.把这个正方形折成两个相等的矩形,再把纸片展平.


第三步,折出内侧矩形的对角线 AB,并把 AB折到图③中所示的AD处,
第四步,展平纸片,按照所得的点D折出 DE,使 DE⊥ND,则图④中就会出现黄金矩形,
问题解决:
(1)图③中AB=________(保留根号);
(2)如图③,判断四边形 BADQ的形状,并说明理由;
(3)请写出图④中所有的黄金矩形,并选择其中一个说明理由.
(4)结合图④.请在矩形 BCDE中添加一条线段,设计一个新的黄金矩形,用字母表示出来,并写出它的长和宽.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线y1=x2﹣4x+4的顶点为A,直线y2=kx﹣2k(k≠0),
(1)试说明直线是否经过抛物线顶点A;
(2)若直线y2交抛物线于点B,且△OAB面积为1时,求B点坐标;
(3)过x轴上的一点M(t,0)(0≤t≤2),作x轴的垂线,分别交y1,y2的图象于点P,Q,判断下列说法是否正确,并说明理由:
①当k>0时,存在实数t(0≤t≤2)使得PQ=3.
②当﹣2<k<﹣0.5时,不存在满足条件的t(0≤t≤2)使得PQ=3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).
(1)将△ABC向下平移5个单位后得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕原点O逆时针旋转90°后得到△A2B2C2,请画出△A2B2C2;
(3)判断以O,A1,B为顶点的三角形的形状.(无须说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线 y=﹣![]() x+4 与坐标轴分别交于 A,B 两点,把△AOB 绕点A 逆时针旋转 90°后得到△AO′B′.
x+4 与坐标轴分别交于 A,B 两点,把△AOB 绕点A 逆时针旋转 90°后得到△AO′B′.
(1)写出点 A 的坐标,点 B 的坐标;
(2)在方格中直接画出△AO′B′;
(3)写出点 O′的坐标;点 B′的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com