
【题目】如图所示,在数轴上有三个点A,B,C,回答下列问题:(注意:本题直接写出答案即可)
![]()
(1)A,C两点间的距离是多少?
(2)数轴上存在点D,点D到点A的距离等于点D到点C的距离问点 D对应的数是多少?
(3)若点E与点B的距离是8,则E点表示的数是什么?
(4)若F点与A点的距离是![]() ,请你写出F点表示的数是多少?(用含字母a的式子表示)
,请你写出F点表示的数是多少?(用含字母a的式子表示)
【答案】(1)5,(2)-0.5,(3)-10或6,(4)-3+a,-3-a
【解析】
(1)根据数轴先找A,C两点表示的数,再用较大的数减去较小的数,即得A,C两点间的距离.
(2)因为D点在A,C的中点,所以可以用A点加C点的数再除以2即可.
(3)根据数轴先找出B点表示的数,点E在B点的左边,用B表示的数为-8,点E在B点的右边,用B点表示的数+8,据此可以得到E点表示的数,同理(4)可以完成.
(1)由数轴可知: A,C两点表示的数分别是-3,2,所以A,C两点的距离是
![]() .
.
(2)![]() ,所以D点在-0.5处.
,所以D点在-0.5处.
(3)B点表示的数是-2,所以E点表示的数是![]() 或
或![]() .
.
(4)A点表示的数是-3,结合数轴上两点距离公式可得F点表示的数是-3+a,-3-a.
故答案为:(1)5,(2)-0.5,(3)-10或6,(4)-3+a,-3-a


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
【题目】已知△ABC,分别以BC,AB,AC为边作等边三角形BCE,ACF,ABD
(1)若存在四边形ADEF,判断它的形状,并说明理由.
(2)存在四边形ADEF的条件下,请你给△ABC添个条件,使得四边形ADEF成为矩形,并说明理由.
(3)当△ABC满足什么条件时四边形ADEF不存在.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、C在线段AD的异侧,点E、F分别是线段AB、CD上的点.已知∠AEG=∠AGE,∠DCG=∠DGC.

(1) 求证:AB∥CD
(2) 若∠AGE+∠AHF=180°,且∠BFC-30°=2∠C,求∠B的度数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一儿童服装商店在销售中发现:某品牌童装平均每天可售出20件,每件盈利40元.为了迎接“六·一”儿童节,商店决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存.经市场调查发现:如果每件童装降价1元,那么平均每天就可多售出2件.要想平均每天销售这种童装上盈利1200元,那么每件童装应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实根x1、x2.
(1)求实数k的取值范围.
(2)若方程两实根x1、x2满足x1+x2=﹣x1x2,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图∠AOB=120°,把三角板60°的角的顶点放在O处.转动三角板(其中OC边始终在∠AOB内部),OE始终平分∠AOD.

(1)(特殊发现)如图1,若OC边与OA边重合时,求出∠COE与∠BOD的度数.
(2)(类比探究)如图2,当三角板绕O点旋转的过程中(其中OC边始终在∠AOB内部),∠COE与∠BOD的度数比是否为定值?若为定值,请求出这个定值;若不为定值,请说明理由.
(3)(拓展延伸)如图3,在转动三角板的过程中(其中OC边始终在∠AOB内部),若OP平分∠COB,请画出图形,直接写出∠EOP的度数(无须证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,AB=AC,过AB上一点D作DE∥AC交BC于点E,以E为顶点,ED为一边,作∠DEF=∠A,另一边EF交AC于点F.
(1)求证:四边形ADEF为平行四边形;
(2)当点D为AB中点时,判断ADEF的形状;
(3)延长图①中的DE到点G,使EG=DE,连接AE,AG,FG,得到图②,若AD=AG,判断四边形AEGF的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,BE平分∠ABC交AD于点E,DF平分∠ADC交BC于点F.
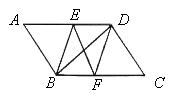
【1】△ABE≌△CDF
【2】若BD⊥EF,则判断四边形EBFD是什么特殊四边形,请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD∥BC,∠EAD=∠C.

(1)试判断AE与CD的位置关系,并说明理由;
(2)若∠FEC=∠BAE,∠EFC=50°,求∠B的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com