
【题目】如图,点B、C在线段AD的异侧,点E、F分别是线段AB、CD上的点.已知∠AEG=∠AGE,∠DCG=∠DGC.

(1) 求证:AB∥CD
(2) 若∠AGE+∠AHF=180°,且∠BFC-30°=2∠C,求∠B的度数
【答案】(1)见解析;(2)50°
【解析】
(1)根据对顶角相等,结合已知条件得出内错角相等,即可得两直线平行;
(2)根据对顶角相等,结合已知条件得出同旁内角互补,则可证出BF∥EC,根据平行线性质得出∠BFC与∠C的关系,结合已知条件求出∠BFC的度数,由两直线平行,同旁内角互补求∠B的度数.
解:(1)∵∠AEG=∠AGE,∠DCG=∠DGC,∠AGE=∠DGC,
∴∠AEG=∠DCG,
∴AB∥CD;
(2)∵∠AGE+∠AHF=180°,∠AGE=∠DGC,
∴∠CGD+∠AHF=180°,
∴BF∥EC;
∴∠BFC+∠C=180°,
∵∠BFC-30°=2∠C,
∴∠BFC=130°,
∵AB∥CD,
∴∠BFC+∠B=180°,
∴∠B=50°.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】如图所示的是用棋子摆成的“![]() ”字形图案.
”字形图案.

(1)填写下表:
图案序号 | ① | ② | ③ | ④ | … | ⑩ |
每个图案中棋子的个数 | 5 | 8 | … |
(2)第![]() 个“
个“![]() ”字形图案中棋子的个数为______.(用含
”字形图案中棋子的个数为______.(用含![]() 的代数式表示)
的代数式表示)
(3)第20个“![]() ”字形图案共有棋子多少个?
”字形图案共有棋子多少个?
(4)计算前20个“![]() ”字形图案中棋子的总个数为______
”字形图案中棋子的总个数为______
查看答案和解析>>
科目:初中数学 来源: 题型:
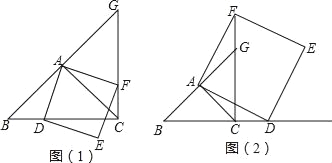
【题目】在△ABC中,AB=AC,∠BAC=90°,点D在射线BC上(与B、C两点不重合),以AD为边作正方形ADEF,使点E与点B在直线AD的异侧,射线BA与直线CF相交于点G.
(1)若点D在线段BC上,如图(1),判断:线段BC与线段CG的数量关系: ,位置关系: .
(2)如图(2),①若点D在线段BC的延长线上,(1)中判断线段BC与线段CG的数量关系与位置关系是否仍然成立,并说明理由;
②当G为CF中点,连接GE,若AB=![]() ,求线段GE的长.
,求线段GE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段抛物线:y=﹣x(x﹣3)(0≤x≤3),记为C1,它与x轴交于点O,A1;
将C1绕点A1旋转180°得C2,交x轴于点A2;
将C2绕点A2旋转180°得C3,交x轴于点A3;
…
如此进行下去,直至得C13.若P(37,m)在第13段抛物线C13上,则m=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 射线
射线![]() ,
,![]() 。
。![]() 是射线
是射线![]() 上一动点,过点
上一动点,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,连结
,连结![]() 。作
。作![]() ,交直线
,交直线![]() 于点
于点![]() ,
,![]() 平分
平分![]() 。
。

(1)若点![]() 都在点
都在点![]() 的右侧。
的右侧。
①求![]() 的度数;
的度数;
②若![]() ,求
,求![]() 的度数。
的度数。
(2)在点![]() 的运动过程中,是否存在这样的情形,使
的运动过程中,是否存在这样的情形,使![]() ,若存在,求出
,若存在,求出![]() 的度数;若不存在,请说明理由。
的度数;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,过AB的中点E作AC的垂线EF,交AD于点M,交CD的延长线于点F.

(1)证明:![]() ;
;
(2)若![]() ,求当形ABCD的周长;
,求当形ABCD的周长;
(3)在没有辅助线的前提下,图中共有_________对相似三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在数轴上有三个点A,B,C,回答下列问题:(注意:本题直接写出答案即可)
![]()
(1)A,C两点间的距离是多少?
(2)数轴上存在点D,点D到点A的距离等于点D到点C的距离问点 D对应的数是多少?
(3)若点E与点B的距离是8,则E点表示的数是什么?
(4)若F点与A点的距离是![]() ,请你写出F点表示的数是多少?(用含字母a的式子表示)
,请你写出F点表示的数是多少?(用含字母a的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CN是等边△![]() 的外角
的外角![]() 内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.
内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.
(1)依题意补全图形;
(2)若![]() ,求
,求![]() 的大小(用含
的大小(用含![]() 的式子表示);
的式子表示);
(3)用等式表示线段![]() ,
, ![]() 与
与![]() 之间的数量关系,并证明.
之间的数量关系,并证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com