
【题目】如图所示的是用棋子摆成的“![]() ”字形图案.
”字形图案.

(1)填写下表:
图案序号 | ① | ② | ③ | ④ | … | ⑩ |
每个图案中棋子的个数 | 5 | 8 | … |
(2)第![]() 个“
个“![]() ”字形图案中棋子的个数为______.(用含
”字形图案中棋子的个数为______.(用含![]() 的代数式表示)
的代数式表示)
(3)第20个“![]() ”字形图案共有棋子多少个?
”字形图案共有棋子多少个?
(4)计算前20个“![]() ”字形图案中棋子的总个数为______
”字形图案中棋子的总个数为______
【答案】(1)填表见解析(2)![]() (3)62(4)670
(3)62(4)670
【解析】
(1)通过观察已知图形可得:每个图形都比其前一个图形多3个棋子,得出摆成第3、4、10个图案需要的棋子数;
(2)由(1)得出规律为摆成第n个图案需要(3n+2)枚棋子;
(3) 把n=20代入计算即可;
(4) 把前20个“![]() ”字形图案中棋子的个数相加即可.
”字形图案中棋子的个数相加即可.
解:(1)
图案序号 | ① | ② | ③ | ④ | … | ⑩ |
每个图案中棋子的个数 | 5 | 8 | 11 | 14 | … | 32 |
(2)由(1)得出规律为摆成第n个图案需要(3n+2)枚棋子;
(3)当n=20时,3n+2=3×20+2=62;
(4)第1个图案有5个棋子,第20个图案有62个棋子,其和是:5+62=67;
第2个图案有8个棋子,第19个图案有59个棋子,其和是:8+59=67;
第3个图案有11个棋子,第18个图案有56个棋子,其和是:11+56=67;
以此类推,前20个图案共有(5+62)×(20÷2)=67×10=670.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】根据下列证明过程填空:
如图,BD⊥AC,EF⊥AC,D、F分别为垂足,且∠1=∠4,求证:∠ADG=∠C

证明:∵BD⊥AC,EF⊥AC
∴∠2=∠3=90°
∴BD∥EF ( )
∴∠4=_____ ( )
∵∠1=∠4
∴∠1=_____
∴DG∥BC ( )
∴∠ADG=∠C( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在点E处,连接DE交AB于点F,当△DEB是直角三角形时,DF的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 已知,如图,点D是△ABC的边AB的中点,四边形BCED是平行四边形.
(1)求证:四边形ADCE是平行四边形;
(2)在△ABC中,若AC=BC,则四边形ADCE是 ;(只写结论,不需证明)
(3)在(2)的条件下,当AC⊥BC时,求证:四边形ADCE是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点E,C在线段BF上,BE=EC=CF,AB∥DE,∠ACB=∠F.
(1)求证:△ABC≌△DEF;
(2)求证:四边形ACFD为平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() 为直线
为直线![]() 上的一点,
上的一点,![]() 为直角,
为直角,![]() 平分
平分![]() .
.
(1)如图1,若![]() ,则
,则![]() ______°.
______°.
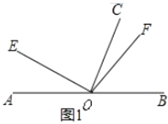
(2)如图1,若![]() ,求
,求![]() 的度数.(用含
的度数.(用含![]() 的代数式表示)
的代数式表示)
(3)如图2,若![]() ,
,![]() 平分
平分![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
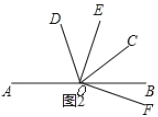
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了对一棵倾斜的古杉树AB进行保护,需测量其长度,如图,在地面上选取一点C,测得∠ACB=45![]() ,AC=24 m,∠BAC=66.5
,AC=24 m,∠BAC=66.5![]() ,求这棵古杉树AB的长度.(结果精确到0.1 m.参考数据:sin66.5
,求这棵古杉树AB的长度.(结果精确到0.1 m.参考数据:sin66.5![]() ≈0.92,cos66.5
≈0.92,cos66.5![]() ≈0.40,tan66.5
≈0.40,tan66.5![]() ≈2.30)
≈2.30)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC,分别以BC,AB,AC为边作等边三角形BCE,ACF,ABD
(1)若存在四边形ADEF,判断它的形状,并说明理由.
(2)存在四边形ADEF的条件下,请你给△ABC添个条件,使得四边形ADEF成为矩形,并说明理由.
(3)当△ABC满足什么条件时四边形ADEF不存在.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、C在线段AD的异侧,点E、F分别是线段AB、CD上的点.已知∠AEG=∠AGE,∠DCG=∠DGC.

(1) 求证:AB∥CD
(2) 若∠AGE+∠AHF=180°,且∠BFC-30°=2∠C,求∠B的度数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com