
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在点E处,连接DE交AB于点F,当△DEB是直角三角形时,DF的长为_____.

【答案】![]() 或
或![]() .
.
【解析】如图1所示;点E与点C′重合时,
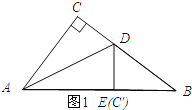
在Rt△ABC中,BC=![]() =4,
=4,
由翻折的性质可知;AE=AC=3、DC=DE,则EB=2,
设DC=ED=x,则BD=4-x,
在Rt△DBE中,DE2+BE2=DB2,即x2+22=(4-x)2,
解得:x=![]() ,
,
∴DE=![]() ;
;
如图2所示:∠EDB=90时,

由翻折的性质可知:AC=AC′,∠C=∠C′=90°,
∵∠C=∠C′=∠CDC′=90°,
∴四边形ACDC′为矩形,
又∵AC=AC′,
∴四边形ACDC′为正方形,
∴CD=AC=3,
∴DB=BC-DC=4-3=1,
∵DE∥AC,
∴△BDE∽△BCA,
∴![]() ,即
,即![]() ,
,
解得:DE=![]() ,
,
点D在CB上运动,∠DBC′<90°,故∠DBC′不可能为直角,
故答案为:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】已知有9张卡片,分别写有1到9这就个数字,将它们的背面朝上洗匀后,任意抽出一张,记卡片上的数字为a,若数a使关于x的不等式组 有解,且使函数
有解,且使函数![]() 在x≥7的范围内y随着x的增大而增大,则这9个数中满足条件的a的值的和是( )
在x≥7的范围内y随着x的增大而增大,则这9个数中满足条件的a的值的和是( )
A. 10 B. 11 C. 12 D. 13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-x2+2x+3与x轴交于A,B两点,与y轴交于点C,点D,C关于抛物线的对称轴对称,直线AD与y轴相交于点E.
(1)求直线AD的解析式;
(2)如图1,直线AD上方的抛物线上有一点F,过点F作FG⊥AD于点G,作FH平行于x轴交直线AD于点H,求△FGH周长的最大值;
(3)如图2,点M是抛物线的顶点,点P是y轴上一动点,点Q是坐标平面内一点,四边形APQM是以PM为对角线的平行四边形,点Q′与点Q关于直线AM对称,连接M Q′,P Q′.当△PM Q′与□APQM重合部分的面积是□APQM面积的![]() 时,求□APQM面积.
时,求□APQM面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,点A的坐标为![]() ,点B坐标为
,点B坐标为![]() 满足
满足![]() .
.
(1)若![]() 没有平方根,判断点A在第几象限并说明理由;
没有平方根,判断点A在第几象限并说明理由;
(2)若点A到![]() 轴的距离是点B到
轴的距离是点B到![]() 轴距离的3倍,求点B的坐标;
轴距离的3倍,求点B的坐标;
(3)点D的坐标为(4,-2),△OAB的面积是△DAB面积的2倍,求点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,等腰直角三角形AOB的直角顶点A在第四象限,顶点B(0,-2),点C(0,1),点D在边AB上,连接CD交OA于点E,反比例函数![]() 的图像经过点D,若△ADE和△OCE的面积相等,则k的值为___________.
的图像经过点D,若△ADE和△OCE的面积相等,则k的值为___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正比例函数![]() 与反比例函数
与反比例函数![]() 的图象分别交于A、C两点,已知点B与点D关于坐标原点O成中心对称,且点B的坐标为
的图象分别交于A、C两点,已知点B与点D关于坐标原点O成中心对称,且点B的坐标为![]() 其中
其中![]() .
.
![]() 四边形ABCD的是______
四边形ABCD的是______![]() 填写四边形ABCD的形状
填写四边形ABCD的形状![]()
![]() 当点A的坐标为
当点A的坐标为![]() 时,四边形ABCD是矩形,求m,n的值.
时,四边形ABCD是矩形,求m,n的值.
![]() 试探究:随着k与m的变化,四边形ABCD能不能成为菱形?若能,请直接写出k的值;若不能,请说明理由.
试探究:随着k与m的变化,四边形ABCD能不能成为菱形?若能,请直接写出k的值;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矗立在莲花山的邓小平雕像气宇轩昂,这是中国第一座以城市雕塑形式竖立的邓小平雕像。铜像由像体AD和底座CD两部分组成。某校数学课外小组在地面的点B处测得点A的仰角∠ABC=67°,点D的仰角∠DBC=30°,已知CD=2米,求像体AD的高度。(最后结果精确到1米,参考数据:sin67°≈0.92,cos67°≈0.39,tan67°≈2.4,![]() ≈1.7)
≈1.7)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的是用棋子摆成的“![]() ”字形图案.
”字形图案.

(1)填写下表:
图案序号 | ① | ② | ③ | ④ | … | ⑩ |
每个图案中棋子的个数 | 5 | 8 | … |
(2)第![]() 个“
个“![]() ”字形图案中棋子的个数为______.(用含
”字形图案中棋子的个数为______.(用含![]() 的代数式表示)
的代数式表示)
(3)第20个“![]() ”字形图案共有棋子多少个?
”字形图案共有棋子多少个?
(4)计算前20个“![]() ”字形图案中棋子的总个数为______
”字形图案中棋子的总个数为______
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com