练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】矗立在莲花山的邓小平雕像气宇轩昂，这是中国第一座以城市雕塑形式竖立的邓小平雕像。铜像由像体AD和底座CD两部分组成。某校数学课外小组在地面的点B处测得点A的仰角∠ABC=67°，点D的仰角∠DBC=30°，已知CD=2米，求像体AD的高度。（最后结果精确到1米，参考数据：sin67°≈0.92，cos67°≈0.39，tan67°≈2.4，≈1.7）

    【答案】6米

    【解析】分析：在Rt△DBC有BC=求得BC的长，在Rt△ABC中由AC=BCtan∠ABC求得AC的长，根据AD=AC-CD可得答案．

    详解：∵在Rt△DBC中，∠DBC=30°，且CD=2米，

    ∴BC==，

    ∵在Rt△ABC中，∠ABC=67°，

    ∴AC=BCtan∠ABC=2tan67°≈8.16，

    则AD=AC-2≈6，

    答：像体AD的高度约为6米．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图：在矩形ABCD中，AD=AB，∠BAD的平分线交BC于点E，DH⊥AE于点H，连接BH并延长交CD于点F，连接DE交BF于点O，有下列结论：①∠AED=∠CED；②OE=OD；③△BEH≌△HDF；④BC﹣CF=2EH；⑤AB=FH．其中正确的结论有（　　）

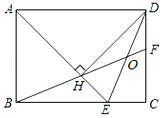
    A. 5个 B. 4个 C. 3个 D. 2个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将平行四边形ABCD折叠，使顶点D落在AB边上的点E处，折痕为AF，下列说法中不正确的是（　　）

    A.EF∥BCB.EF＝AEC.BE＝CFD.AF＝BC

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB=90°，AB=5，AC=3，点D是BC上一动点，连接AD，将△ACD沿AD折叠，点C落在点E处，连接DE交AB于点F，当△DEB是直角三角形时，DF的长为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题情景：如图1，在等腰直角三角形ABC中∠ACB＝90°，BC＝a．将AB绕点B顺时针旋转90°得到线段BD，连接CD，过点D作△BCD的BC边上的高DE．

    易证△ABC≌△BDE，从而得到△BCD的面积为．

    简单应用：如图2，在Rt△ABC中，∠ACB＝90°，BC＝a，将边AB绕点B顺时针旋转90°得到线段BD，连接CD，用含a的代数式表示△BCD的面积，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】 已知，如图，点D是△ABC的边AB的中点，四边形BCED是平行四边形．

    （1）求证：四边形ADCE是平行四边形；

    （2）在△ABC中，若AC＝BC，则四边形ADCE是　 　；（只写结论，不需证明）

    （3）在（2）的条件下，当AC⊥BC时，求证：四边形ADCE是正方形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知点E，C在线段BF上，BE＝EC＝CF，AB∥DE，∠ACB＝∠F．

    (1)求证：△ABC≌△DEF；

    (2)求证：四边形ACFD为平行四边形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了对一棵倾斜的古杉树AB进行保护，需测量其长度，如图，在地面上选取一点C，测得∠ACB＝45，AC＝24 m，∠BAC＝66.5，求这棵古杉树AB的长度．（结果精确到0.1 m．参考数据：sin66.5≈0.92，cos66.5≈0.40，tan66.5≈2.30）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是抛物线形拱桥，当拱顶离水面2m时，水面宽4m，则水面下降1m时，水面宽度增加_____m．

    查看答案和解析>>

    同步练习册答案