
【题目】如图:在矩形ABCD中,AD=![]() AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,有下列结论:①∠AED=∠CED;②OE=OD;③△BEH≌△HDF;④BC﹣CF=2EH;⑤AB=FH.其中正确的结论有( )
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,有下列结论:①∠AED=∠CED;②OE=OD;③△BEH≌△HDF;④BC﹣CF=2EH;⑤AB=FH.其中正确的结论有( )
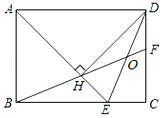
A. 5个 B. 4个 C. 3个 D. 2个
【答案】B
【解析】分析: 先证明△ABE和△ADH是等腰直角三角形,得出AD=AE,AB=AH=DH=DC,得出∠ADE=∠AED,即可得出①正确;先证出OE=OH,同理:OD=OH,得出OE=OD,②正确;由ASA证出△BEH≌△HDF,得出③正确;过H作HK⊥BC于K,可知![]() ,HK=KE,得出
,HK=KE,得出![]() ,BC=2HK+2HE=FC+2HE得出④正确.
,BC=2HK+2HE=FC+2HE得出④正确.
详解: ∵四边形ABCD是矩形,
∴![]() AB=DC,AD∥BC,
AB=DC,AD∥BC,
∴∠ADE=∠CED,
∵∠BAD的平分线交BC于点E,
∴![]()
∴△ABE和△ADH是等腰直角三角形,
∴![]()
∵![]()
∴AD=AE,AB=AH=DH=DC,
∴∠ADE=∠AED,
∴∠AED=∠CED,
∴①正确;
∵![]()
∴![]() ,
,
∵![]()
∴![]() ,
,
∴![]() ,
,
∴∠OHE=∠AED,
∴OE=OH,
同理:OD=OH,
∴OE=OD,
∴②正确;
∵![]()
∴∠HBE=∠FHD,
在△BEH和△HDF中,
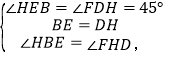
∴△BEH≌△HDF(ASA),
∴③正确;
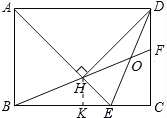
BCCF=2HE正确,过H作HK⊥BC于K,
可知![]() ,HK=KE,
,HK=KE,
由上知HE=EC,
∴![]() ,
,
又![]() ,HE
,HE
故![]() ,BC=2HK+2HE=FC+2HE
,BC=2HK+2HE=FC+2HE
∴④正确;
⑤不正确;
故选B.


科目:初中数学 来源: 题型:
【题目】某校计划组织师生共300人参加一次大型公益活动,如果租用6辆大客车和5辆小客车,恰好全部坐满,已知每辆大客车的乘客座位数比小客车多17个.
(1)求每辆大客车和每辆小客车的乘客座位数;
(2)由于最后参加活动的人数增加了30人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,且所有参加活动的师生都有座位,求租用小客车数量的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高新一中初中校区名校+教育联合体主题美术展在西安高新区都市之门举办,学校组织七年级部分学生乘车参观展览,若用2辆小客车和1辆大客车,则每次可运送学生95人;若用1辆小客车和2辆大客车,则每次可运送学生115人(注意:每辆小客车和大客车都坐满).
(1)每辆小客车和大客车各能坐多少人?
(2)若现在要运送500名学生,计划租用小客车![]() 辆,大客车
辆,大客车![]() 辆,一次送完,且恰好每辆车都坐满,请你帮学校设计出所有的租车方案.
辆,一次送完,且恰好每辆车都坐满,请你帮学校设计出所有的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知有9张卡片,分别写有1到9这就个数字,将它们的背面朝上洗匀后,任意抽出一张,记卡片上的数字为a,若数a使关于x的不等式组 有解,且使函数
有解,且使函数![]() 在x≥7的范围内y随着x的增大而增大,则这9个数中满足条件的a的值的和是( )
在x≥7的范围内y随着x的增大而增大,则这9个数中满足条件的a的值的和是( )
A. 10 B. 11 C. 12 D. 13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,是假命题的是( )
A. 在△ABC中,若∠A:∠B:∠C=1:2:3,则△ABC是直角三角形
B. 在△ABC中,若a2=(b+c) (b-c),则△ABC是直角三角形
C. 在△ABC中,若∠B=∠C=∠A,则△ABC是直角三角形
D. 在△ABC中,若a:b:c=5:4:3,则△ABC是直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解青少年形体情况,现随机抽查了某市若干名初中学生坐姿、站姿、走姿的好坏情况.我们对测评数据作了适当处理(如果一个学生有一种以上不良姿势,以他最突出的一种作记载),并将统计结果绘制了如下两幅不完整的统计图,请你根据图中所给信息解答下列问题:
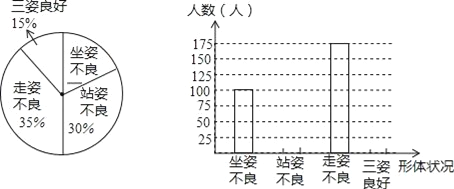
(1)请将两幅统计图补充完整;
(2)请问这次被抽查形体测评的学生一共是多少人?
(3)如果全市有5万名初中生,那么全市初中生中,坐姿和站姿不良的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在眉山市开展城乡综合治理的活动中,需要将![]() 、
、![]() 、
、![]() 三地的垃圾50立方米、40立方米、50立方米全部运往垃圾处理场
三地的垃圾50立方米、40立方米、50立方米全部运往垃圾处理场![]() 、
、![]() 两地进行处理.已知运往
两地进行处理.已知运往![]() 地的数量比运往
地的数量比运往![]() 地的数量的2倍少10立方米.
地的数量的2倍少10立方米.
(1)求运往两地的数量各是多少立方米?
(2)若![]() 地运往
地运往![]() 地
地![]() 立方米
立方米![]() 为整数),
为整数),![]() 地运往
地运往![]() 地30立方米,
地30立方米,![]() 地运往
地运往![]() 地的数量小于
地的数量小于![]() 地运往
地运往![]() 地的2倍.其余全部运往
地的2倍.其余全部运往![]() 地,且
地,且![]() 地运往
地运往![]() 地不超过12立方米,则
地不超过12立方米,则![]() 、
、![]() 两地运往
两地运往![]() 、
、![]() 两地哪几种方案?
两地哪几种方案?
(3)已知从![]() 、
、![]() 、
、![]() 三地把垃圾运往
三地把垃圾运往![]() 、
、![]() 两地处理所需费用如下表:
两地处理所需费用如下表:
|
|
| |
运往 | 22 | 20 | 20 |
运往 | 20 | 22 | 21 |
在(2)的条件下,请说明哪种方案的总费用最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-x2+2x+3与x轴交于A,B两点,与y轴交于点C,点D,C关于抛物线的对称轴对称,直线AD与y轴相交于点E.
(1)求直线AD的解析式;
(2)如图1,直线AD上方的抛物线上有一点F,过点F作FG⊥AD于点G,作FH平行于x轴交直线AD于点H,求△FGH周长的最大值;
(3)如图2,点M是抛物线的顶点,点P是y轴上一动点,点Q是坐标平面内一点,四边形APQM是以PM为对角线的平行四边形,点Q′与点Q关于直线AM对称,连接M Q′,P Q′.当△PM Q′与□APQM重合部分的面积是□APQM面积的![]() 时,求□APQM面积.
时,求□APQM面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矗立在莲花山的邓小平雕像气宇轩昂,这是中国第一座以城市雕塑形式竖立的邓小平雕像。铜像由像体AD和底座CD两部分组成。某校数学课外小组在地面的点B处测得点A的仰角∠ABC=67°,点D的仰角∠DBC=30°,已知CD=2米,求像体AD的高度。(最后结果精确到1米,参考数据:sin67°≈0.92,cos67°≈0.39,tan67°≈2.4,![]() ≈1.7)
≈1.7)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com