
����Ŀ����üɽ�п�չ�����ۺ������Ļ�У���Ҫ��![]() ��
��![]() ��
��![]() ���ص�����50�����ס�40�����ס�50������ȫ����������������
���ص�����50�����ס�40�����ס�50������ȫ����������������![]() ��
��![]() ���ؽ��д�������֪����
���ؽ��д�������֪����![]() �ص�����������
�ص�����������![]() �ص�������2����10�����ף�
�ص�������2����10�����ף�
��1�����������ص��������Ƕ��������ף�
��2����![]() ������
������![]() ��
��![]() ������
������![]() ��������
��������![]() ������
������![]() ��30�����ף�
��30�����ף�![]() ������
������![]() �ص�����С��
�ص�����С��![]() ������
������![]() �ص�2��������ȫ������
�ص�2��������ȫ������![]() �أ���
�أ���![]() ������
������![]() �ز�����12�����ף���
�ز�����12�����ף���![]() ��
��![]() ��������
��������![]() ��
��![]() �����ļ��ַ�����
�����ļ��ַ�����
��3����֪��![]() ��
��![]() ��
��![]() ���ذ���������
���ذ���������![]() ��
��![]() ���ش�������������±���
���ش�������������±���
|
|
| |
���� | 22 | 20 | 20 |
���� | 20 | 22 | 21 |
�ڣ�2���������£���˵�����ַ������ܷ������٣�
���𰸡���1��������D��90�����ף�����E��50�����ף���2������������3����һ�ַ������ܷ������٣�
��������
��1��������E��x�����ף���������г�����x�ķ��̣����x��ֵ���ɣ�
��2���������г�����a��һԪһ�β���ʽ�飬���a��ȡֵ��Χ���ٸ���a�������ɵó�a��ֵ������������𰸣�
��3�����ݣ�1���е����ַ����������ü��ɣ�
��1��������E��x�����ף�������ã�x+2x-10=140��
��ã�x=50��
��2x-10=90��
�𣺹�����D��90�����ף�����E��50�����ף�
��2��������ɵã�
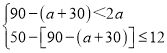 ��
��
��ã�20��a��22��
��a��������
��a=21��22��
�����������ַ�����
��һ�֣�A������D��21�����ף�����E��29�����ף�
C������D��39�����ף�����E��11�����ף�
�ڶ��֣�A������D��22�����ף�����E��28�����ף�
C������D��38�����ף�����E��12�����ף�
��3����һ�ַ���������ã�
22��21+20��29+30��20+22��10+39��20+11��21=2873��Ԫ����
�ڶ��ַ���������ã�
22��22+28��20+30��20+22��10+38��20+12��21=2876��Ԫ����
���ԣ���һ�ַ������ܷ������٣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABC������ƽ���ڣ��������������ֱ�ΪA��0��3����B��3��4����C��2��2�����������������У�ÿ��С�����εı߳���1����λ���ȣ�
��1��������ABC����ƽ��4����λ��������ƽ��1����λ�õ��ġ�A1B1C1����ֱ��д��C1������ꣻ
��2��������ABC�Ƶ�A˳ʱ�뷽����ת90����õ��ġ�A2B2C2����ֱ��д��C2������ꣻ

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ijʦ��ԺУ��Ƹһ�����ظڽ�ʦ�����Լס��ҡ���������λ��ѡ�˽��������Ժͱ��ԣ����ǵijɼ������
��ѡ�� | �� | �� | �� | �� | |
���Գɼ� | ���� | 86 | 91 | 90 | 83 |
���� | 90 | 83 | 83 | 92 | |
����¼�ó�����Ϊ�����ʦ���Եijɼ�Ӧ�ñȱ��Եijɼ�����Ҫ�����ֱ�������6��4��Ȩ.�������˸��Ե�ƽ���ɼ�������Ϊ��¼ȡ�� ��
A.��B.��C.��D.��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AD=![]() AB����BAD��ƽ���߽�BC�ڵ�E��DH��AE�ڵ�H������BH���ӳ���CD�ڵ�F������DE��BF�ڵ�O�������н��ۣ��١�AED=��CED����OE=OD���ۡ�BEH�ա�HDF����BC��CF=2EH����AB=FH��������ȷ�Ľ����У�������
AB����BAD��ƽ���߽�BC�ڵ�E��DH��AE�ڵ�H������BH���ӳ���CD�ڵ�F������DE��BF�ڵ�O�������н��ۣ��١�AED=��CED����OE=OD���ۡ�BEH�ա�HDF����BC��CF=2EH����AB=FH��������ȷ�Ľ����У�������
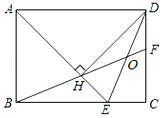
A. 5�� B. 4�� C. 3�� D. 2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
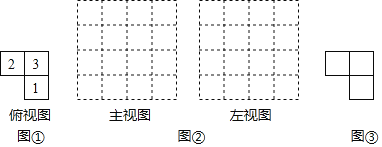
����Ŀ���ɼ�����ͬ�ı߳�Ϊ1��С�������ɵļ�����ĸ���ͼ��ͼ�٣����е����ֱ�ʾ��λ�õ�С������ĸ�����
��1���������淽��ֽͼ���зֱ���������������ͼ������ͼ��
��2����������ͼ�������ϼ�����ı����Ϊ���ٸ�ƽ����λ���������������
��3��������С�������ɵļ�����ĸ���ͼ���䣬��ͼ�ۣ���λ�õ�С������������Ըı䣨����Ŀ���䣩��������������ϼ������еı��������������������ͼ�٣���������д��ͼ�۵��������У�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������֤��������գ�
��ͼ��BD��AC��EF��AC��D��F�ֱ�Ϊ���㣬�ҡ�1=��4����֤����ADG=��C

֤������BD��AC��EF��AC
���2=��3=90��
��BD��EF ( )
���4=_____ ( )
�ߡ�1=��4
���1=_____
��DG��BC ( )
���ADG=��C( )
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��ѧ����С�飬������ֽ��ΪѧУ��һ��յ����ֲ���������£���k������ֲ�ڵ�Pk(xk,yk)��������x1=1��y1=1����k��2ʱ��![]() ,
,![]()
![]() ��[a]��ʾ�Ǹ�ʵ��a���������֣�����[2.6]=2��[0.2]=0�����˷��������2018������ֲ�������Ϊ( )
��[a]��ʾ�Ǹ�ʵ��a���������֣�����[2.6]=2��[0.2]=0�����˷��������2018������ֲ�������Ϊ( )
A.��3��2018��B.��2��2019��C.��2��403��D.��3��404��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�۵���ʹ����D����AB���ϵĵ�E�����ۺ�ΪAF������˵���в���ȷ���ǣ�������

A.EF��BCB.EF��AEC.BE��CFD.AF��BC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��E��C���߶�BF�ϣ�BE��EC��CF��AB��DE����ACB����F��
(1)��֤����ABC�ա�DEF��
(2)��֤���ı���ACFDΪƽ���ı��Σ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com