练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知有9张卡片，分别写有1到9这就个数字，将它们的背面朝上洗匀后，任意抽出一张，记卡片上的数字为a，若数a使关于x的不等式组 有解，且使函数 在x≥7的范围内y随着x的增大而增大，则这9个数中满足条件的a的值的和是（　　）

    A. 10 B. 11 C. 12 D. 13

    【答案】D

    【解析】解：解不等式4x≥3（x+1），可得：x≥3，解不等式2x﹣＜a，可得：x＜．∵不等式组 有解，∴＞3，解得a＞5．∵y=x2﹣2ax=（x﹣a）2﹣a2，∴对称轴为x=a，开口向上，∴当x≥a时，y随x的增大而增大．∵函数y=x2﹣2ax在x≥7的范围内y随x增大而增大，∴a≤7，综上可知5＜a≤7．∵a为1到9这九个数字中的一个，∴a的值为6或7，∴满足条件的a的值之和=6+7=13．故选D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】（1）操作发现：

    如图①，在中，，点D是BC上一点，沿AD折叠，使得点C恰好落在AB上的点E处.请写出AB、AC、CD之间的关系________________________________；

    （2）问题解决：

    如图②，若（1）中；，其他条件不变，请猜想AB、AC、CD之间的关系，并证明你的结论；

    （3）类比探究：

    如图③，在四边形ABCD中，，，，，连接AC、点E是CD上一点，沿AE折叠，使得点D正好落在AC上的F处，若，求DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么这两次拐弯的角度是（ ）

    A. 第一次向右拐40, 第二次向左拐140

    B. 第一次向左拐40, 第二次向右拐40

    C. 第一次向左拐40, 第二次向左拐140

    D. 第一次向右拐40, 第二次向右拐40°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，两个形状、大小完全相同的含有30°、60°的直角三角板如图①放置，PA、PB与直线MN重合，且三角板PAC、三角板PBD均可绕点P逆时针旋转．

    （1）直接写出∠DPC的度数．

    （2）如图②，在图①基础上，若三角板PAC的边PA从PN处开始绕点P逆时针旋转，转速为5°/秒，同时三角板PBD的边PB从PM处开始绕点P逆时针旋转，转速为1°/秒，（当PA转到与PM重合时，两三角板都停止转动），在旋转过程中，当PC与PB重合时，求旋转的时间是多少？

    （3）在（2）的条件下，PC、PB、PD三条射线中，当其中一条射线平分另两条射线的夹角时，请直接写出旋转的时间．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】莒南县欲从某师范院校招聘一名“特岗教师”，对甲、乙、丙、丁四位候选人进行了面试和笔试，他们的成绩如表：

    候选人

    甲

    乙

    丙

    丁

    测试成绩

    面试

    86

    91

    90

    83

    笔试

    90

    83

    83

    92

    根据录用程序，作为人民教师面试的成绩应该比笔试的成绩更重要，并分别赋予它们6和4的权.根据四人各自的平均成绩，你认为将录取（ ）

    A.甲B.乙C.丙D.丁

    查看答案和解析>>

    科目：初中数学 来源： 题型：

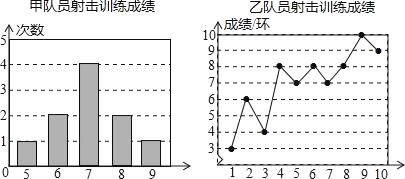
    【题目】甲、乙两名队员参加射击训练（各射击10次），成绩分别被制成下列两个统计图：

    根据以上信息，整理分析数据如下表：

    平均成绩/环

    中位数/环

    众数/环

    方差/环2

    甲

    a

    7

    7

    1.2

    乙

    7

    b

    8

    c

    （1）求出表格中a，b，c的值；

    （2）分别运用表中的统计量，简要分析这两名队员的射击成绩，若选派其中一名参赛，你认为应选哪名队员？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图：在矩形ABCD中，AD=AB，∠BAD的平分线交BC于点E，DH⊥AE于点H，连接BH并延长交CD于点F，连接DE交BF于点O，有下列结论：①∠AED=∠CED；②OE=OD；③△BEH≌△HDF；④BC﹣CF=2EH；⑤AB=FH．其中正确的结论有（　　）

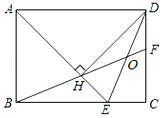
    A. 5个 B. 4个 C. 3个 D. 2个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】根据下列证明过程填空：

    如图，BD⊥AC，EF⊥AC，D、F分别为垂足，且∠1=∠4，求证：∠ADG=∠C

    证明：∵BD⊥AC，EF⊥AC

    ∴∠2=∠3=90°

    ∴BD∥EF ( )

    ∴∠4=_____ ( )

    ∵∠1=∠4

    ∴∠1=_____

    ∴DG∥BC ( )

    ∴∠ADG=∠C( )

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB=90°，AB=5，AC=3，点D是BC上一动点，连接AD，将△ACD沿AD折叠，点C落在点E处，连接DE交AB于点F，当△DEB是直角三角形时，DF的长为_____．

    查看答案和解析>>

    同步练习册答案