
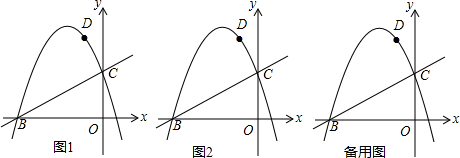
分析 (1)先求出点B坐标,把B、D两点坐标代入抛物线解析式解方程组即可.
(2)如图1中,求出CD的长,作MN⊥x轴于N,由MN∥CO得$\frac{CO}{MN}$=$\frac{BC}{BM}$=$\frac{BO}{BN}$,求出MN,BN即可解决问题.
(3)如图3中,作FK⊥OB于K,OT⊥BC于T,连接OF,先证明OT平分∠COF,利用△OTC∽△BOC得$\frac{CT}{CO}$=$\frac{CO}{BC}$,求出CT,CF,由FK∥CO得$\frac{FK}{CO}$=$\frac{BF}{BC}$=$\frac{BK}{BO}$,由此求出点F坐标,再求出直线PE,列方程组求出点P坐标,发现PQ∥x轴,求出点Q坐标,再说明△DMQ绕点D顺时针旋转90°后得到△DGH,点G在线段BC上,点H在x轴上,DH⊥OB,最后求出BG,GH的长即可解决问题.
解答 解:(1)∵直线y=$\frac{k}{2}$x+2k交x轴于点B,令y=0得x=-4,
∴点B坐标(-4,0),
把B(-4,0),D(-$\frac{2}{3}$,$\frac{10}{3}$)代入抛物线解析式得$\left\{\begin{array}{l}{-12-4b+c=0}\\{-\frac{1}{3}-\frac{2}{3}b+c=\frac{10}{3}}\end{array}\right.$解得$\left\{\begin{array}{l}{b=-\frac{5}{2}}\\{c=2}\end{array}\right.$,
∴抛物线解析式为y=-$\frac{3}{4}$x2-$\frac{5}{2}$x+2.
(2)如图1中,∵点C(0,2)在直线y=y=$\frac{k}{2}$x+2k上,∴2k=2,k=1,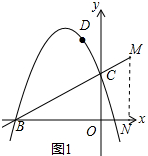
∴直线BC为y=$\frac{1}{2}$x+2,
∵CD=$\sqrt{(\frac{2}{3})^{2}+(\frac{10}{3}-2)^{2}}$=$\frac{2\sqrt{5}}{3}$,BC=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
作MN⊥x轴于N,
∵MN∥CO,
∴$\frac{CO}{MN}$=$\frac{BC}{BM}$=$\frac{BO}{BN}$,
∴$\frac{2}{MN}$=$\frac{2\sqrt{5}}{\frac{8\sqrt{5}}{3}}$=$\frac{4}{BM}$,
∴MN=$\frac{8}{3}$,NB=$\frac{16}{3}$,ON=BN-OB=$\frac{4}{3}$
∴点M坐标($\frac{4}{3}$,$\frac{8}{4}$).
(3)如图2中,作FK⊥OB于K,OT⊥BC于T,连接OF.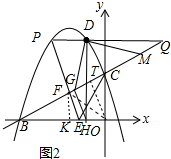 ∵∠EFC=90°,∠EOC=90°,
∵∠EFC=90°,∠EOC=90°,
∴∠EFC+∠EOC=180°,
∴E、F、C、O四点共圆,
∴∠FEC=∠FOC=2∠CBO,
∵∠CBO+∠BCO=90°,∠COT+∠BCO=90°,
∴∠COT=∠CBO,
∴∠TOC=∠TOF,
∵∠TFO+∠TOF=90°,∠TCO+∠TOC=90°,
∴∠TFO=∠TCO,
∴OF=OC=2,
∵∠OTC=∠BOC,∠TCO=∠BCO,
∴△OTC∽△BOC,
∴$\frac{CT}{CO}$=$\frac{CO}{BC}$,
∴CT=$\frac{2\sqrt{5}}{5}$,
∴GC=2TC=$\frac{4\sqrt{5}}{5}$,
∵FK∥CO,
∴$\frac{FK}{CO}$=$\frac{BF}{BC}$=$\frac{BK}{BO}$,
∴$\frac{FK}{2}$=$\frac{\frac{6\sqrt{5}}{5}}{2\sqrt{5}}$=$\frac{BK}{4}$
∴FK=$\frac{6}{5}$,BK=$\frac{12}{5}$,KO=OB-BK=$\frac{8}{5}$,
∴点F坐标(-$\frac{8}{5}$,$\frac{6}{5}$),
∵PF⊥BC,直线BC为y=$\frac{1}{2}$x+2,
∴可以假设直线PE为y=-2x+b,点F代入得到b=-2,
∴直线PE为y=-2x-2,
由$\left\{\begin{array}{l}{y=-2x-2}\\{y=-\frac{3}{4}{x}^{2}-\frac{5}{2}x+2}\end{array}\right.$解得$\left\{\begin{array}{l}{x=-\frac{8}{3}}\\{y=\frac{10}{3}}\end{array}\right.$,或$\left\{\begin{array}{l}{x=-2}\\{y=2}\end{array}\right.$,
∵点P在第二象限,
∴点P坐标(-$\frac{8}{3}$,$\frac{10}{3}$),
∵点D(-$\frac{2}{3}$,$\frac{10}{3}$),
∴PD∥x轴,
∴点Q坐标为($\frac{8}{3}$,$\frac{10}{3}$),
∴PD=2,DQ=$\frac{10}{3}$,
∵直线DC为y=-2x+2,直线BC为y=$\frac{1}{2}$x+2,
∴DC⊥BC,
∵DC=CM,
∴△DCM是等腰直角三角形,
∴∠DMC=45°,∠DMQ=135°,
∴△DMQ绕点D顺时针旋转90°后得到△DGH,点G在线段BC上,
∵DQ=$\frac{10}{3}$,点D纵坐标为$\frac{10}{3}$,
∴点H在x轴上,DH⊥OB,
∵∠DGM=∠DMG=45°,∠DGH=∠DMQ=135°,
∴∠HGQ=90°,
∵BG=BC-CG=2$\sqrt{5}$-$\frac{2\sqrt{5}}{3}$=$\frac{4\sqrt{5}}{3}$,QC=$\sqrt{(\frac{8}{3})^{2}+(\frac{10}{3}-2)^{2}}$=$\frac{4\sqrt{5}}{3}$,
∴GH=MQ=CQ-CM=$\frac{4\sqrt{5}}{3}$-$\frac{2\sqrt{5}}{3}$=$\frac{2\sqrt{5}}{3}$,
∴S△BGH=$\frac{1}{2}$•BG•GH=$\frac{1}{2}$×$\frac{4\sqrt{5}}{3}$×$\frac{2\sqrt{5}}{3}$=$\frac{20}{9}$.
点评 本题考查二次函数、一次函数的有关知识、旋转变换、平行线分线段成比例定理、相似三角形的判定和性质等知识,发现△OFC是等腰三角形是解题的关键,学会利用方程组求两个函数图象的交点坐标,第三个问题求出点P坐标是解题的关键,题目比较难需要正确画出图形,是数形结合的好题目.


科目:初中数学 来源: 题型:选择题
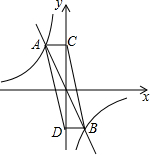 如图,直线y=kx(k<0)与双曲线y=$\frac{-2}{x}$交于点A、B,AC⊥y轴于C,BD⊥y轴于D,连接AD、BC,则四边形ABCD的面积为( )
如图,直线y=kx(k<0)与双曲线y=$\frac{-2}{x}$交于点A、B,AC⊥y轴于C,BD⊥y轴于D,连接AD、BC,则四边形ABCD的面积为( )| A. | 2 | B. | 4 | C. | 1 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
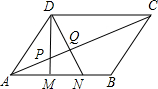 如图,在平行四边形ABCD中,M、N为AB的三等分点,DM、DN分别交AC于P、Q两点,则AP:PC=1:3,AP:PQ:CQ=5:3:12.
如图,在平行四边形ABCD中,M、N为AB的三等分点,DM、DN分别交AC于P、Q两点,则AP:PC=1:3,AP:PQ:CQ=5:3:12.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
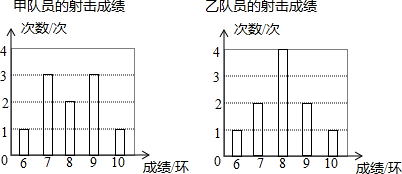
| 姓名 | 平均成绩 | 众数 | 中位数 | 极差 | 方差 | 标准差 |
| 甲 | 8环 | 7环与9环 | 8环 | 4环 | 14 | $\sqrt{14}$ |
| 乙 | 8环 | 8环 | 8环 | 4环 | 12 | 2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
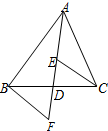 如图,△ABC中,AB=AC,AD是角平分线,BE=CF,则下列说法中正确的有( )
如图,△ABC中,AB=AC,AD是角平分线,BE=CF,则下列说法中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com