Question

已知关于x一元二次方程有两个不相等的实数根

（1）求k取值范围；

（2）当k最小的整数时，求抛物线的顶点坐标以及它与x轴的交点坐标；

（3）将（2）中求得的抛物线在x轴下方的部分沿x轴翻折到x轴上方，图象的其余部分不变，得到一个新图象．请你画出这个新图象，并求出新图象与直线有三个不同公共点时m值．

 

 

Answer 1

（1）k＞-1；（2）（1，-4）；（-1，0），（3，0）；（3）画图见解析，1或．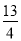

【解析】

试题分析：（1）根据一元二次方程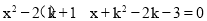有两个不相等的实数根，可知根的判别式△＞0，即可求出k的取值范围.

（2）根据k的取值范围可得当k=0时，为k最小的整数，进而可求出顶点坐标以及它与x轴的交点坐标.

（3）由（2）画出此函数图象后，可发现，若直线与新函数有3个交点，可以有两种情况：

①直线经过原二次函数与x轴的交点A（即左边的交点），可将A点坐标代入直线的解析式中，即可求出m的值；

②原二次函数图象x轴以下部分翻折后，所得部分图象仍是二次函数，该二次函数与原函数开口方向相反、对称轴相同、与x轴的交点坐标相同，可据此判断出该函数的解析式，若直线与新函数图象有三个交点，那么当直线与该二次函数只有一个交点时，恰好满足这一条件，那么联立直线与该二次函数的解析式，可化为一个关于x的一元二次方程，那么该方程的判别式△=0，根据这一条件可确定m的取值．

试题解析：（1）由题意，得，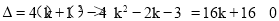

∴k＞-1，

∴k的取值范围为k＞-1.

（2）∵k＞-1，且k取最小的整数，∴k=0．

∴.

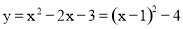则抛物线的顶点坐标为（1，-4）.

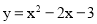∵的图象与x轴相交，

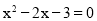∴，∴解得：x=-1或3.

∴抛物线与x轴相交于A（-1，0），B（3，0）；

（3）翻折后所得新图象如图所示．

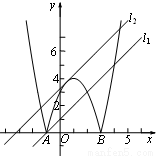
平移直线y=x+m知：直线位于l1和l2时，它与新图象有三个不同的公共点．

①当直线位于l1时，此时l1过点A（-1，0），

∴0=-1+m，即m=1．

②当直线位于l2时，此时l2与函数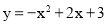的图象有一个公共点，

∴方程x+m=-x2+2x+3，即x2-x-3+m=0有两个相等实根.

∴△=1-4（m-3）=0，即m=．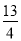

当m=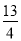时，x1=x2=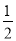满足-1≤x≤3，

由①②知m=1或m=．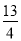

考点：1.抛物线与x轴的交点；2.二次函数图象与几何变换；3.一元二次方程根的判别式；4.分类思想的应用．