
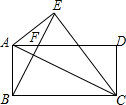
 如图,在矩形ABCD中,BC=2BA=8,将矩形ABCD沿AC所在直线翻折使△ABC与△AEC重合,连接BE,BE交AD于点F,则线段EF的长为$\frac{6\sqrt{5}}{5}$.
如图,在矩形ABCD中,BC=2BA=8,将矩形ABCD沿AC所在直线翻折使△ABC与△AEC重合,连接BE,BE交AD于点F,则线段EF的长为$\frac{6\sqrt{5}}{5}$. 分析 首先由勾股定理求得AC的长度,然后证明△ABF∽△BCA,求得AF=2,接下来证明△ABC∽△BOC,可求得OE=$\frac{8\sqrt{5}}{5}$,最后△AOF∽△ADC,可求得OF=$\frac{2\sqrt{5}}{5}$,从而可求得EF的长.
解答 解:如图所示: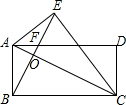
在Rt△ABC中,AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{4}^{2}+{8}^{2}}$=4$\sqrt{5}$.
由翻折的性质可知:AC⊥BE,OB=OE,
∴∠OBC+∠BCA=90°
又∵∠ABF+∠FBC=90°,
∴∠ABF=∠ACB.
又∵∠BAF=∠CBA=90°,
∴△ABF∽△BCA.
∴$\frac{AF}{AB}=\frac{AB}{BC}$,即$\frac{AF}{4}=\frac{4}{8}$.
∴AF=2.
∵∠ABF=∠ACB,∠BOC=∠ABC=90°,
∴△ABC∽△BOC.
∴.$\frac{OB}{AB}=\frac{BC}{AC}$,即$\frac{OB}{4}=\frac{8}{4\sqrt{5}}$.
∴OB=$\frac{8\sqrt{5}}{5}$.
∴OE=$\frac{8\sqrt{5}}{5}$.
∵∠OAF=∠DAC,∠AOF=∠ADC=90°,
∴△AOF∽△ADC.
∴$\frac{OF}{AF}=\frac{DC}{AC}$,$\frac{OF}{2}=\frac{4}{4\sqrt{5}}$.
∴OF=$\frac{2\sqrt{5}}{5}$.
EF=OE-OF=$\frac{8\sqrt{5}}{5}-\frac{2\sqrt{5}}{5}$=$\frac{6\sqrt{5}}{5}$.
故答案为:$\frac{6\sqrt{5}}{5}$.
点评 本题主要考查的是相似三角形的性质和判定、翻折变换,证得△ABF∽△BCA、△ABC∽△BOC、△AOF∽△ADC是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 线”,点P为“
线”,点P为“ 点”.
点”. 点”的坐标;
点”的坐标; 线”,并说明理由;
线”,并说明理由; 线”,求k的取值范围.
线”,求k的取值范围. 点”的⊙C的“
点”的⊙C的“ 线”,求r的值.
线”,求r的值.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2,3) | B. | (-3,-2) | C. | (-3,2) | D. | (2,3) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
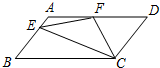 如图,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,联结EF、CF,那么下列结论中一定成立的个数是( )
如图,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,联结EF、CF,那么下列结论中一定成立的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x-3y=3}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+1=3}\\{y+2=-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+2y=3}\\{3x-2y=-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{x}{y}=3}\\{x-y=4}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com