
分析 (1)根据分式的除法法则进行计算即可;
(2)先找最简公分母,然后利用分式的基本性质通分,把异分母分式化为同分母分式,再进行加减.
解答 解:(1)原式=$\frac{x}{x+\frac{1-x}{\frac{{x}^{2}-1}{x}}}$
=$\frac{x}{x-\frac{x}{1+x}}$
=$\frac{1+x}{x}$;
(2)原式=$\frac{{x}^{2}+3x+9}{(x-3)({x}^{2}+3x+9)}$-$\frac{6x}{x(x+3)(x-3)}$-$\frac{x-1}{2(x+3)}$
=$\frac{1}{x-3}$-$\frac{6}{(x+3)(x-3)}$-$\frac{x-1}{2(x+3)}$
=$\frac{2(x+3)}{2(x+3)(x-3)}$-$\frac{12}{2(x+3)(x-3)}$-$\frac{(x-1)(x-3)}{2(x+3)(x-3)}$
=$\frac{-{x}^{2}+6x-9}{2(x+3)(x-3)}$
=$\frac{-(x-3)^{2}}{2(x+3)(x-3)}$
=$\frac{3-x}{2(x+3)}$.
点评 本题考查的是分式的混合运算,熟知分式混合运算的法则是解答此题的关键.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
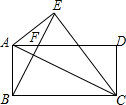 如图,在矩形ABCD中,BC=2BA=8,将矩形ABCD沿AC所在直线翻折使△ABC与△AEC重合,连接BE,BE交AD于点F,则线段EF的长为$\frac{6\sqrt{5}}{5}$.
如图,在矩形ABCD中,BC=2BA=8,将矩形ABCD沿AC所在直线翻折使△ABC与△AEC重合,连接BE,BE交AD于点F,则线段EF的长为$\frac{6\sqrt{5}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
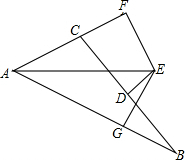 如图,已知AE平分∠BAC,ED垂直平分BC,EF⊥AC,EG⊥AB,垂足分别是点F、G.求证:
如图,已知AE平分∠BAC,ED垂直平分BC,EF⊥AC,EG⊥AB,垂足分别是点F、G.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 1号 | 2号 | 3号 | 4号 | 5号 | 合计 | |
| 甲 | 100 | 98 | 110 | 89 | 103 | 500 |
| 乙 | 89 | 100 | 95 | 119 | 97 | 500 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com