
【题目】如图,在等腰△ABC中,AB=AC,∠A=20°,AB上一点D使AD=BC,过点D作DE∥BC且DE=AB,连接EC,则∠DCE的度数为( )
A.80°
B.70°
C.60°
D.45°
【答案】B
【解析】解:如图所示,连接AE.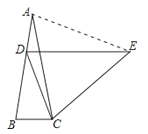
∵AE=DE,
∴∠ADE=∠DAE,
∵DE∥BC,
∴∠DAE=∠ADE=∠B,
∵AB=AC,∠BAC=20°,
∴∠DAE=∠ADE=∠B=∠ACB=80°,
在△ADE与△CBA中,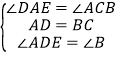 ,
,
∴△ADE≌△CBA(ASA),
∴AE=AC,∠AED=∠BAC=20°,
∵∠CAE=∠DAE﹣∠BAC=80°﹣20°=60°,
∴△ACE是等边三角形,
∴CE=AC=AE=DE,∠AEC=∠ACE=60°,
∴△DCE是等腰三角形,
∴∠CDE=∠DCE,
∴∠DEC=∠AEC﹣∠AED=40°,
∴∠DCE=∠CDE=(180﹣40°)÷2=70°.
故选B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】阅读材料:若m2﹣2mn+2n2﹣8n+16=0,求m、n的值.
解:∵m2﹣2mn+2n2﹣8n+16=0,∴(m2﹣2mn+n2)+(n2﹣8n+16)=0,
∴(m﹣n)2+(n﹣4)2=0,又∵(m﹣n)2≥0,(n﹣4)2≥0,
∴![]() , ∴n=4,m=4.
, ∴n=4,m=4.
请解答下面的问题:
(1)已知x2﹣2xy+2y2+6y+9=0,求xy﹣x2的值;
(2)已知△ABC的三边长a、b、c都是互不相等的正整数,且满足a2+b2﹣4a﹣18b+85=0,求△ABC的最大边c的值;
(3)已知a2+b2=12,ab+c2﹣16c+70=0,求a+b+c的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一块均匀的不等边三角形的铁板,它的重心在( )
A. 三角形的三条角平分线的交点 B. 三角形的三条高线的交点
C. 三角形的三条中线的交点 D. 三角形的三条边的垂直平分线的交点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(﹣2,5)的对应点A′的坐标是
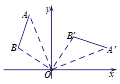
A. (2,5) B. (5,2) C. (4, ![]() ) D. (
) D. (![]() ,4)
,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AC=BC,AB=4,∠ACB=90°,以AB的中点D为圆心DC长为半径作![]() 圆DEF,设∠BDF=α(0°<α<90°),当α变化时图中阴影部分的面积为 (
圆DEF,设∠BDF=α(0°<α<90°),当α变化时图中阴影部分的面积为 (![]() 圆:∠EDF=90°,
圆:∠EDF=90°,![]() 圆的面积=
圆的面积=![]()
![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,AB=AC,射线BM、BN在∠ABC内部,分别交线段AC于点G、H.
(1)如图1,若∠ABC=60°、∠MBN=30°,作AE⊥BN于点D,分别交BC、BM于点E、F.
①求证:CE=AG;
②若BF=2AF,连接CF,求∠CFE的度数;
(2)如图2,点E为BC上一点,AE交BM于点F,连接CF,若∠BFE=∠BAC=2∠CFE,直接写出![]() 的结果
的结果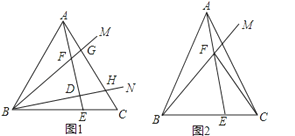
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com