
【题目】已知在△ABC中,AB=AC,射线BM、BN在∠ABC内部,分别交线段AC于点G、H.
(1)如图1,若∠ABC=60°、∠MBN=30°,作AE⊥BN于点D,分别交BC、BM于点E、F.
①求证:CE=AG;
②若BF=2AF,连接CF,求∠CFE的度数;
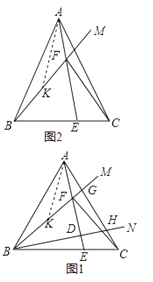
(2)如图2,点E为BC上一点,AE交BM于点F,连接CF,若∠BFE=∠BAC=2∠CFE,直接写出![]() 的结果
的结果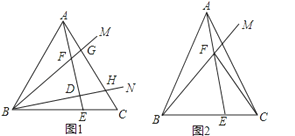
【答案】解:(1)①∵AB=AC,∠ABC=60°
∴△ABC为等边三角形,
则∠BAC=∠ACB=60°,AB=CA,
∵AD⊥BN,∠MBN=30°,
∴∠BFD=∠AFG=60°,
∵∠ABF+∠BAF=60°,
∠BAF+∠EAC=60°
∴∠EAC=∠GBA
在△GBA与△EAC中,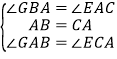 ,
,
∴△GBA≌△EAC,
∴CE=AG;
②如图1,取BF的中点K连接AK,
∵BF=2AF,
∴AF=BK=FK=![]() BF,
BF,
∴△FAK是等腰三角形,
∴∠FAK=∠FKA,
∵∠BFD=∠FAK+∠FKA=2∠AKF,
∵∠BFD=60°,
∴∠AKF=![]() ∠BFD=300
∠BFD=300
∵△GBA≌△EAC,
∴AG=CE,BG=AE,∠AGB=∠AEC,
∴KG=BG﹣BK=AE﹣AF=FE,
在△GAK与△EFC中,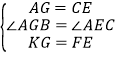 ,
,
∴△GAK≌△EFC,
∴∠CFE=∠AKF,
∴∠CFE=∠AKF=30°;
(2)如图2,在BF上取BK=AF,连接AK,
∵∠BFE=∠BAF+∠ABF,
∵∠BFE=∠BAC,
∴∠BAF+∠EAC=∠BAF+ABF,
∴∠EAC=∠FBA,
在△ABK与△ACF中, ,
,
∴△ABK≌△AFC,
∴S△ABK=S△ACF , ∠AKB=∠AFC,
∵∠BFE=2∠CFE,
∴∠BFE=2∠AKF,
∵∠BFE=2∠AKF=∠AKF+KAF,
∴∠AKF=∠KAF,
∴△FAK是等腰三角形,
∴AF=FK,
∴BK=AF=FK,
∴S△ABK=S△AFK ,
∵S△ABF=S△ABK+S△AFK=2S△ABK=2S△ACF ,
∴![]() =
=![]() .
.
故答案为:![]() .
.
【解析】(1)①由AB=AC,∠ABC=60°得到△ABC为等边三角形,根据等边三角形的性质得到∠BAC=∠ACB=60°,AB=CA,求得∠BFD=∠AFG=60°,推出∠EAC=∠GBA证得△GBA≌△EAC,根据全等三角形的性质即可得到结论;②如图1,取BF的中点K连接AK,由BF=2AF,推出△FAK是等腰三角形,根据等腰三角形的性质得到∠FAK=∠FKA,求得∠AKF=![]() ∠BFD=300 , 根据全等三角形的性质得到AG=CE,BG=AE,∠AGB=∠AEC,推出△GAK≌△EFC,根据全等三角形的性质得到∠CFE=∠AKF即可得到结论;
∠BFD=300 , 根据全等三角形的性质得到AG=CE,BG=AE,∠AGB=∠AEC,推出△GAK≌△EFC,根据全等三角形的性质得到∠CFE=∠AKF即可得到结论;
(2)如图2,在BF上取BK=AF,连接AK,推出∠EAC=∠FBA,根据全等三角形的性质得到S△ABK=S△ACF , ∠AKB=∠AFC,证得△FAK是等腰三角形,根据等腰三角形的性质得到AF=FK,即可得到结论.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,∠CDB=2∠ABD,∠ABC=105°,∠A=∠C=45°. 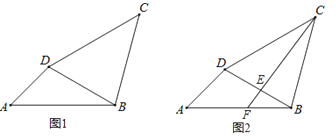
(1)求∠ABD;
(2)求证:CD=AB;
(3)如图2,过点C作CF⊥BD于点E,交AB于点F,若AB=3![]() , 则BF+BE等于多少?
, 则BF+BE等于多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC,∠A=20°,AB上一点D使AD=BC,过点D作DE∥BC且DE=AB,连接EC,则∠DCE的度数为( )
A.80°
B.70°
C.60°
D.45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个质地均匀的小正方体,六个面分别标有数字“1”“2”“3”“4”“5”“6”. 连续两次抛掷小正方体,观察每次朝上一面的数字.
(1)请用列表格或画树状图的方法列举出两次抛掷的所有可能结果;
(2)求出第二次抛掷的数字大于第一次抛掷的数字的概率;
(3)求两次抛掷的数字之和为5的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高中的篮球队球员中,一、二年级的成员共有8人,三年级的成员有3人,一、二年级的成员身高(单位:厘米)如下:
172,172,174,174,176,176,178,178.
若队中所有成员的平均身高为178厘米,则队中三年级成员的平均身高为( )
A. 178 B. 181 C. 183 D. 186
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com