
科目:初中数学 来源: 题型:填空题
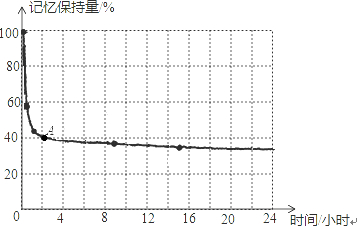
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
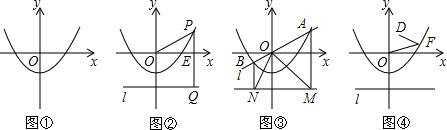
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
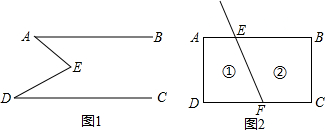
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
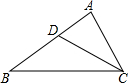 如图所示,要使得△ABC∽△ACD,只需增加条件( )
如图所示,要使得△ABC∽△ACD,只需增加条件( )| A. | $\frac{AC}{CD}$=$\frac{AB}{BC}$ | B. | CD2=AD•DB | C. | ∠B=∠BCD | D. | ∠ADC=∠ACB |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
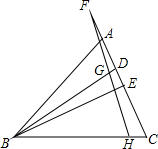 如图,△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE,交BD于点G,交BC于点H;下列结论:
如图,△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE,交BD于点G,交BC于点H;下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
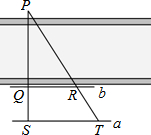 如图,为了估计河的宽度,在河的对岸选定一个目标点P,在近岸取点Q和S,使点P,Q,S在一条直线上,且直线PS与河垂直,在过点S且与PS垂直的直线a上选择适当的点T,PT与过点Q且与PS垂直的直线b的交点为R.如果QS=60m,ST=120m,QR=80m,则河的宽度PQ为( )
如图,为了估计河的宽度,在河的对岸选定一个目标点P,在近岸取点Q和S,使点P,Q,S在一条直线上,且直线PS与河垂直,在过点S且与PS垂直的直线a上选择适当的点T,PT与过点Q且与PS垂直的直线b的交点为R.如果QS=60m,ST=120m,QR=80m,则河的宽度PQ为( )| A. | 40m | B. | 60m | C. | 120m | D. | 180m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com