
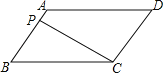
【题目】如图,ABCD中,AB=2,BC=4,∠B=60°,点P是四边形上的一个动点,则当△PBC为直角三角形时,BP的长为_____.
【答案】2或2![]() 或
或![]() .
.
【解析】
分两种情况:(1)①当∠BPC=90°时,作AM⊥BC于M,求出BM=![]() AB=1,AM=
AB=1,AM=![]() BM=
BM=![]() ,由勾股定理求出AC,由勾股定理的逆定理证出△ABC是直角三角形,∠BAC=90°,得出点P与A重合即可;②当∠BPC=90°,点P在边AD上,CP=CD=AB=2时,由勾股定理求出BP即可;
,由勾股定理求出AC,由勾股定理的逆定理证出△ABC是直角三角形,∠BAC=90°,得出点P与A重合即可;②当∠BPC=90°,点P在边AD上,CP=CD=AB=2时,由勾股定理求出BP即可;
(2)当∠BCP=90°时,CP=AM=![]() ,由勾股定理求出BP即可.
,由勾股定理求出BP即可.
解:分两种情况:
(1)①当∠BPC=90°时,
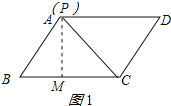
作AM⊥BC于M,如图1所示,
∵∠B=60°,
∴∠BAM=30°,
∴BM=![]() AB=1,
AB=1,
∴AM=![]() BM=
BM=![]() ,CM=BC﹣BM=4﹣1=3,
,CM=BC﹣BM=4﹣1=3,
∴AC=![]() =2
=2![]() ,
,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,∠BAC=90°,
∴当点P与A重合时,∠BPC=∠BAC=90°,
∴BP=BA=2;
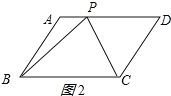
②当∠BPC=90°,
点P在边AD上,CP=CD=AB=2时,
BP=![]() =
=![]() =2
=2![]() ;
;
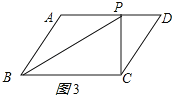
(2)当∠BCP=90°时,如图3所示:
则CP=AM=![]() ,
,
∴BP=![]() =
=![]() ;
;
综上所述:当△PBC为直角三角形时,BP的长为2或2![]() 或
或![]() .
.
故答案为:2或2![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】记某商品销售单价为x元,商家销售此种商品每月获得的销售利润为y元,且y是关于x的二次函数.已知当商家将此种商品销售单价分别定为55元或75元时,他每月均可获得销售利润1800元;当商家将此种商品销售单价定为80元时,他每月可获得销售利润1550元,则y与x的函数关系式是( )
A.y=﹣(x﹣60)2+1825B.y=﹣2(x﹣60)2+1850
C.y=﹣(x﹣65)2+1900D.y=﹣2(x﹣65)2+2000
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的.连接BE、CF相交于点D.
(1)求证:BE=CF.
(2)当四边形ACDE为菱形时,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着新能源汽车的发展,某公交公司将用新能源公交车淘汰某一条线路上“冒黑烟”较严重的燃油公交车,计划购买A型和B型新能源公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需300万元;若购买A型公交车2辆,B型公交车1辆,共需270万元,
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该条线路上A型和B型公交车每辆年均载客量分别为80万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1000万元,且确保这10辆公交车在该线路的年均载客量总和不少于900万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的小布袋中装有4个质地、大小完全相同的小球,它们分别标有数字0,1,2,3,小明从布袋里随机摸出一个小球,记下数字为![]() ,小红在剩下的3个小球中随机摸出一个小球,记下数字为
,小红在剩下的3个小球中随机摸出一个小球,记下数字为![]() ,这样确定了点
,这样确定了点![]() 的坐标
的坐标![]() .
.
(1)画树状图或列表,写出点![]() 所有可能的坐标;
所有可能的坐标;
(2)小明和小红约定做一个游戏,其规则为:若![]() 在第一象限,则小明胜;否则,小红胜;这个游戏公平吗?请你作出判断并说明理由.
在第一象限,则小明胜;否则,小红胜;这个游戏公平吗?请你作出判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
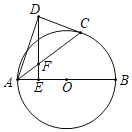
【题目】如图,AB是⊙O的直径,点C在半圆上,点D在圆外,DE⊥AB于点E交AC于点F,且DF=CD
(1)求证:CD是⊙O的切线;
(2)若点F是AC的中点,DF=2EF=2![]() ,求⊙O半径.
,求⊙O半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
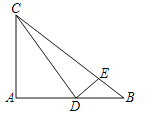
【题目】在Rt△ABC中,∠A=90°,AB=4,AC=3,D为AB边上一动点(点D与点A、B不重合),联结CD,过点D作DE⊥DC交边BC于点E.
(1)如图,当ED=EB时,求AD的长;
(2)设AD=x,BE=y,求y关于x的函数解析式并写出函数定义域;
(3)把△BCD沿直线CD翻折得△CDB',联结AB',当△CAB'是等腰三角形时,直接写出AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
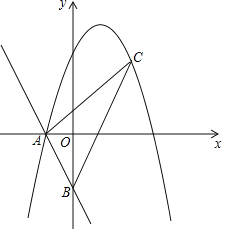
【题目】一次函数y=﹣2x﹣2分别与x轴、y轴交于点A、B.顶点为(1,4)的抛物线经过点A.
(1)求抛物线的解析式;
(2)点C为第一象限抛物线上一动点.设点C的横坐标为m,△ABC的面积为S.当m为何值时,S的值最大,并求S的最大值;
(3)在(2)的结论下,若点M在y轴上,△ACM为直角三角形,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=AB,把△ABC绕点A顺时针旋转得到△ADE(点B、C分别对应点D、E),BD和CE交于点F.
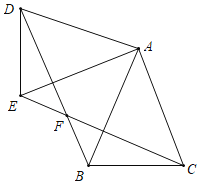
(1)求证:CE=BD;
(2)若AB=2,∠BAC=45°,当四边形ADFC是平行四边形时,求BF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com