
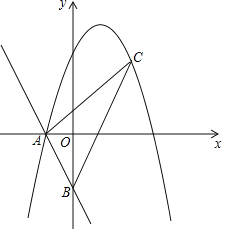
【题目】一次函数y=﹣2x﹣2分别与x轴、y轴交于点A、B.顶点为(1,4)的抛物线经过点A.
(1)求抛物线的解析式;
(2)点C为第一象限抛物线上一动点.设点C的横坐标为m,△ABC的面积为S.当m为何值时,S的值最大,并求S的最大值;
(3)在(2)的结论下,若点M在y轴上,△ACM为直角三角形,请直接写出点M的坐标.
【答案】(1)y=﹣x2+2x+3
(2)当m=2时,S的值最大,最大值为![]()
(3)(0,﹣1)、(0,5)、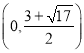 或
或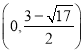
【解析】
(1)设抛物线的解析式为![]() ,代入点A的坐标即可求解.
,代入点A的坐标即可求解.
(2)连接0C,可得点![]() 根据一次函数y=-2x-2得出点A、B的坐标,然后利用三角形面积公式得出
根据一次函数y=-2x-2得出点A、B的坐标,然后利用三角形面积公式得出![]() 的表达式,利用二次函数的表达式即可求解.
的表达式,利用二次函数的表达式即可求解.
(3)设M(0,n),已知A、C点坐标可求出直线AC的解析式,分三种情况,当AC⊥MC,求出M点坐标,当AC⊥AM时,求出M点坐标,当AM⊥MC时,求出M点坐标.
(1)一次函数y=﹣2x﹣2与x轴交于点A,则A的坐标为(﹣1,0),
∵抛物线的顶点为(1,4),
∴设抛物线解析式为y=a(x﹣1)2+4,
∵抛物线经过点A(﹣1,0),
∴0=a(﹣1﹣1)2+4,
∴a=﹣1,
∴抛物线解析式为y=﹣(x﹣1)2+4=﹣x2+2x+3;
(2)连接OC,点C为第一象限抛物线上一动点,点C的横坐标为m,
∴C(m,﹣m2+2m+3),
一次函数y=﹣2x﹣2与y轴交于点B,则OB=2,
∵A的坐标为(﹣1,0),
∴OA=1,
∴![]() ,
,![]()
![]()
![]()
∴当m=2时,S的值最大,最大值为![]() .
.
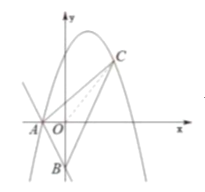
(3)设M(0,n),
∵A(﹣1,0),C(2,3),
∴直线AC的解析式为y=x+1,
①当AC⊥MC时,![]() =﹣1,
=﹣1,
∴n=5,
∴M(0,5);
②当AC⊥AM时,n=﹣1,
∴M(0,﹣1);
③当AM⊥MC时,![]() n=﹣1,
n=﹣1,
∴n=![]()
∴M(0,![]() )或M(0,
)或M(0,![]() );
);
综上所述:点M的坐标为(0,﹣1)、(0,5)、(0,![]() )或(0,
)或(0,![]() ).
).
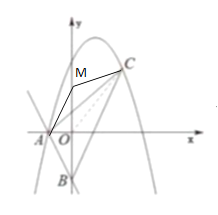


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知![]() 和
和![]() 均为等腰三角形,
均为等腰三角形,![]() ,
,![]() ,将这两个三角形放置在一起.
,将这两个三角形放置在一起.
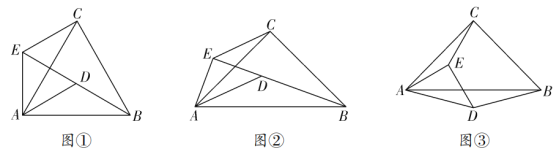
(1)问题发现
如图①,当![]() 时,点
时,点![]() 、
、![]() 、
、![]() 在同一直线上,连接
在同一直线上,连接![]() ,则
,则![]() 的度数为__________,线段
的度数为__________,线段![]() 、
、![]() 、
、![]() 之间的数量关系是__________;
之间的数量关系是__________;
(2)拓展探究
如图②,当![]() 时,点
时,点![]() 、
、![]() 、
、![]() 在同一直线上,连接
在同一直线上,连接![]() .请判断
.请判断![]() 的度数及线段
的度数及线段![]() 、
、![]() 、
、![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
(3)解决问题
如图③,![]() ,
,![]() ,
,![]() ,连接
,连接![]() 、
、![]() ,在
,在![]() 绕点
绕点![]() 旋转的过程中,当
旋转的过程中,当![]() 时,请直接写出
时,请直接写出![]() 的长
的长
查看答案和解析>>
科目:初中数学 来源: 题型:
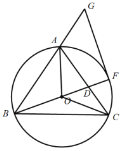
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的外接圆,连结OA、OB、OC,延长BO与AC交于点D,与
的外接圆,连结OA、OB、OC,延长BO与AC交于点D,与![]() 交于点F,延长BA到点G,使得
交于点F,延长BA到点G,使得![]() ,连接FG.
,连接FG.
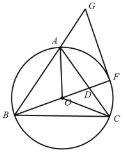
备用图
(1)求证:FG是![]() 的切线;
的切线;
(2)若![]() 的半径为4.
的半径为4.
①当![]() ,求AD的长度;
,求AD的长度;
②当![]() 是直角三角形时,求
是直角三角形时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年2月22日深圳地铁10号线华南城站试运行,预计今年6月正式开通.在地铁的建设中,某段轨道的铺设若由甲乙两工程队合做,12天可以完成,共需工程费用27720元;已知乙队单独完成这项工程所需时间是甲队单独完成这项工程所需时间的1.5倍,且甲队每天的工程费用比乙队多250元.
(1)求甲、乙两队单独完成这项工程各需多少天?
(2)若工程管理部门决定从这两个队中选一个队单独完成此项工程,从节约资金的角度考虑,应选择哪个工程队?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,A,B为定点,A(2,﹣3),B(4,﹣3),定直线l∥AB,P是l上一动点,l到AB的距离为6,M,N分别为PA,PB的中点下列说法中:
①线段MN的长始终为1;②△PAB的周长固定不变;
③△PMN的面积固定不变; ④若存在点Q使得四边形APBQ是平行四边形,则Q到MN所在直线的距离必为9.
其中正确的说法是_____.
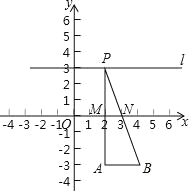
查看答案和解析>>
科目:初中数学 来源: 题型:
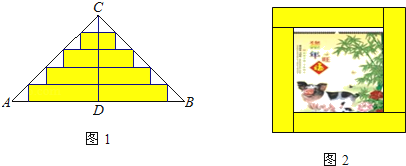
【题目】如图1,△ABC是一张等腰直角三角形彩色纸,AC=BC,将斜边上的高CD五等分,然后裁出4张宽度相等的长方形纸条.若用这4张纸条刚好可以为一幅正方形美术作品镶边(纸条不重叠),如图2,则正方形美术作品与镶边后的作品的面积之比为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=![]() ,AD=3,点E从点B出发,沿BC边运动到点C,连结DE,点E作DE的垂线交AB于点F.在点E的运动过程中,以EF为边,在EF上方作等边△EFG,则边EG的中点H所经过的路径长是( )
,AD=3,点E从点B出发,沿BC边运动到点C,连结DE,点E作DE的垂线交AB于点F.在点E的运动过程中,以EF为边,在EF上方作等边△EFG,则边EG的中点H所经过的路径长是( )

A. 2 ![]() B. 3
B. 3![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
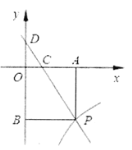
【题目】已知:如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() )的图象交于点
)的图象交于点![]() .
.![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() . 一次函数的图象分别交
. 一次函数的图象分别交![]() 轴、
轴、![]() 轴于点
轴于点![]() 、点
、点![]() ,且
,且![]() ,
,![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求一次函数与反比例函数的解析式;
(3)根据图象写出当![]() 取何值时,一次函数的值小于反比例函数的值?
取何值时,一次函数的值小于反比例函数的值?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com