
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的外接圆,连结OA、OB、OC,延长BO与AC交于点D,与
的外接圆,连结OA、OB、OC,延长BO与AC交于点D,与![]() 交于点F,延长BA到点G,使得
交于点F,延长BA到点G,使得![]() ,连接FG.
,连接FG.
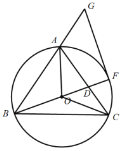
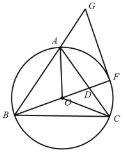
备用图
(1)求证:FG是![]() 的切线;
的切线;
(2)若![]() 的半径为4.
的半径为4.
①当![]() ,求AD的长度;
,求AD的长度;
②当![]() 是直角三角形时,求
是直角三角形时,求![]() 的面积.
的面积.
【答案】(1)见解析;(2)①![]() ,②当
,②当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
【解析】
(1)连接AF,由圆周角定理的推论可知![]() ,根据等腰三角形的性质及圆周角定理的推论可证
,根据等腰三角形的性质及圆周角定理的推论可证![]() ,
,![]() ,从而可得
,从而可得![]() ,然后根据切线的判定方法解答即可;
,然后根据切线的判定方法解答即可;
(2)①连接CF,根据“SSS”证明![]() ,由全等三角形及等腰三角形的性质可得
,由全等三角形及等腰三角形的性质可得![]() ,进而可证
,进而可证![]() ,由平行线分线段成比例定理可证
,由平行线分线段成比例定理可证![]() ,可求
,可求![]() ,然后由相交弦定理求解即可;
,然后由相交弦定理求解即可;
②分两种情况求解即可,(i)当![]() 时,(ii)当
时,(ii)当![]() 时.
时.
(1)连接AF,
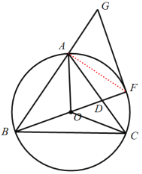
∵BF为![]() 的直径,
的直径,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() .
.
又∵OF为半径,
∴FG是![]() 的切线.
的切线.
(2)①连接CF,
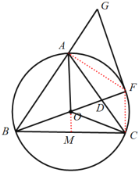
则![]() ,
,
∵AB=AC,OB=OC,OA=OA,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∵半径是4,![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ,
,
又由相交弦定理可得:![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() (舍负);
(舍负);
(2)②∵![]() 为直角三角形,
为直角三角形,![]() 不可能等于
不可能等于![]() .
.
∴(i)当![]() 时,则
时,则![]() ,
,
由于![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ;
;
(ii)当![]() 时,
时,
∵![]() ,∴
,∴![]() 是等腰直角三角形,∴
是等腰直角三角形,∴![]() ,
,
延长AO交BC于点M,
∵AB=AC,
∴弧AB=弧AC,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
【题目】图 1、图 2 均是 6×6 的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为 1,点 A、B、C、D 均在格点上.在图 1、图 2 中,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上,不要求写出画法.
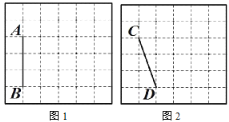
(1)在图 1 中以线段 AB 为边画一个△ABM,使∠ABM=45°,且△ABM 的面积为 6;
(2)在图 2 中以线段 CD 为边画一个四边形 CDEF,使∠CDE=∠CFE=90°,且四边形 CDEF 的面积为 8.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=mx2﹣4mx+n(m>0)与x轴交于A、B两点(点A在原点左侧),与y轴交于点C,且OB=2OA,连接AC、BC.
(1)求A、B两点的坐标;
(2)将线段AC绕点A旋转60°得到线段AC',若点C'在抛物线的对称轴上,求出此时抛物线的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为45°,测得底部C的角为60°,此时航拍无人机与该建筑物的水平距离AD为80m,那么该建筑物的高度BC为_____m(结果保留根号).
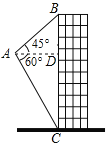
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接体育中考,某校九(1)班的体育老师对全班45名学生进行了一次体育模拟测试(得分均为整数),成绩满分为10分,该班的体育委员根据这次测试成绩,制作了统计图和分析表如下:
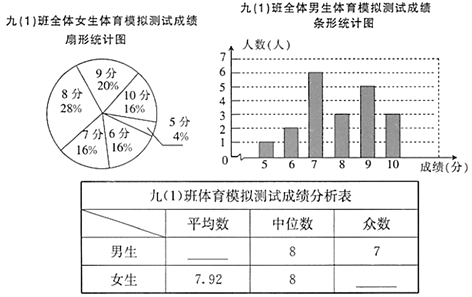
根据以上信息,解答下列问题.
(1)这个班共有男生_________人,女生有____________人.
(2)请你补全九(1)班体育模拟测试成绩分析表.
(3)你认为在这次体育模拟测试中,九(1)班的全体男生和全体女生,谁的表现更好一些?请写出一条支持你的看法的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
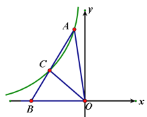
【题目】如图,在△AOB中,OC平分∠AOB,![]() ,反比例函数
,反比例函数![]() 图像经过点A、C两点,点B在x轴上,若△AOB的面积为7,则k的值为( )
图像经过点A、C两点,点B在x轴上,若△AOB的面积为7,则k的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家教育部为支援西部教育发展,计划投入大量资金在西部各省修建A,B两类大型图书馆共10个![]() 若修建A类图书馆1个,B类图书馆2个,共需400万元;若修建A类图书馆2个,B类图书馆1个,共需350万元.
若修建A类图书馆1个,B类图书馆2个,共需400万元;若修建A类图书馆2个,B类图书馆1个,共需350万元.
(1)求修建A类和B类图书馆每个各需多少万元?
(2)预计在该计划上A类和B类图书馆年均阅览量分别为60万人次和100万人次![]() 若教育部投入A类和B类图书馆的总费用不超过1200万元,且确保这10个图书馆的年均阅览量总和不少于680万人次.如果你是领导,从节约投资费用考虑,请设计出可行的方案.
若教育部投入A类和B类图书馆的总费用不超过1200万元,且确保这10个图书馆的年均阅览量总和不少于680万人次.如果你是领导,从节约投资费用考虑,请设计出可行的方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com