
【题目】已知:如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() )的图象交于点
)的图象交于点![]() .
.![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() . 一次函数的图象分别交
. 一次函数的图象分别交![]() 轴、
轴、![]() 轴于点
轴于点![]() 、点
、点![]() ,且
,且![]() ,
,![]() .
.
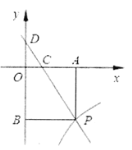
(1)求点![]() 的坐标;
的坐标;
(2)求一次函数与反比例函数的解析式;
(3)根据图象写出当![]() 取何值时,一次函数的值小于反比例函数的值?
取何值时,一次函数的值小于反比例函数的值?
【答案】(1)![]() 的坐标为
的坐标为![]() ;(2)
;(2)![]() ,
, ![]() ; (3)当
; (3)当![]() 时,一次函数的值小于反比例函数的值.
时,一次函数的值小于反比例函数的值.
【解析】
(1)本题需先根据题意一次函数与y轴的交点,从而得出D点的坐标.
(2)本题需先根据在Rt△COD和Rt△CAP中,![]() ,OD=3,再根据S△DBP=27,从而得出BP得长和P点的坐标,即可求出结果.
,OD=3,再根据S△DBP=27,从而得出BP得长和P点的坐标,即可求出结果.
(3)根据图形从而得出x的取值范围即可.
解:(1)∵一次函数![]() 与
与![]() 轴相交,
轴相交,
∴令![]() ,解得
,解得![]() ,
,
∴![]() 的坐标为
的坐标为![]() ;
;
(2)∵![]() ,
,
∴![]() ,
,
又∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,即
,即![]() ,
,
∴![]() ,
,
故![]() ,
,
把![]() 坐标代入
坐标代入![]() ,得到
,得到![]() ,
,
则一次函数的解析式为:![]() ;
;
把![]() 坐标代入反比例函数解析式得
坐标代入反比例函数解析式得![]() ,
,
则反比例解析式为:![]() ;
;
(3)如图:
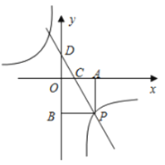
根据图象可得: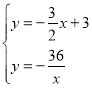 ,
,
解得:![]() 或
或 ![]()
故直线与双曲线的两个交点为![]() ,
,![]() ,
,
∵![]() ,
,
∴当![]() 时,一次函数的值小于反比例函数的值.
时,一次函数的值小于反比例函数的值.


科目:初中数学 来源: 题型:
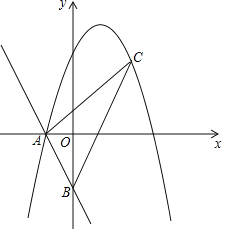
【题目】一次函数y=﹣2x﹣2分别与x轴、y轴交于点A、B.顶点为(1,4)的抛物线经过点A.
(1)求抛物线的解析式;
(2)点C为第一象限抛物线上一动点.设点C的横坐标为m,△ABC的面积为S.当m为何值时,S的值最大,并求S的最大值;
(3)在(2)的结论下,若点M在y轴上,△ACM为直角三角形,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=AB,把△ABC绕点A顺时针旋转得到△ADE(点B、C分别对应点D、E),BD和CE交于点F.
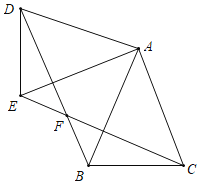
(1)求证:CE=BD;
(2)若AB=2,∠BAC=45°,当四边形ADFC是平行四边形时,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小元步行从家去火车站,走到 6 分钟时,以同样的速度回家取物品,然后从家乘出租车赶往火车站,结果比预计步行时间提前了3 分钟.小元离家路程S(米)与时间t(分钟)之间的函数图象如图,从家到火车站路程是( )

A.1300 米B.1400 米C.1600 米D.1500 米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:四边形 ABCD 内接于⊙O,连接 AC、BD,∠BAD+2∠ACB=180°.
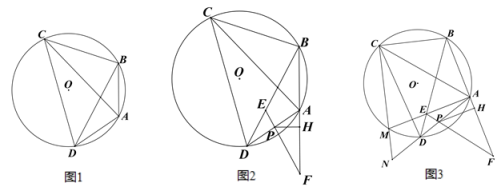
(1)如图 1,求证:点 A 为弧 BD 的中点;
(2)如图 2,点 E 为弦 BD 上一点,延长 BA 至点 F,使得 AF=AB,连接 FE 交 AD 于点 P,过点 P 作 PH⊥AF 于点 H,AF=2AH+AP,求证:AH:AB=PE:BE;
(3)在(2)的条件下,如图 3,连接 AE,并延长 AE 交⊙O 于点 M,连接 CM,并延长 CM 交 AD 的延长线于点 N,连接 FD,∠MND=∠MED,DF=12﹒sin∠ACB,MN=![]() ,求 AH 的长.
,求 AH 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于()
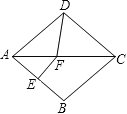
A.50°B.60°C.70°D.80°
查看答案和解析>>
科目:初中数学 来源: 题型:
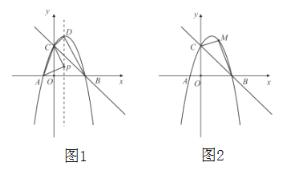
【题目】已知,如图1,抛物线![]() 过
过![]() 三点,顶点为点
三点,顶点为点![]() ,连接
,连接![]() ,点
,点![]() 为抛物线对称轴上一点,连接
为抛物线对称轴上一点,连接![]() ,直线
,直线![]() 过点
过点![]() 两点.
两点.
(1)求抛物线![]() 及直线
及直线![]() 的函数解析式;
的函数解析式;
(2)求![]() 的最小值;
的最小值;
(3)求证:![]() ∽
∽![]() ;
;
(4)如图2,若点![]() 是在抛物线
是在抛物线![]() 上且位于第一象限内的一动点,请直接写出
上且位于第一象限内的一动点,请直接写出![]() 面积的最大值及此时点
面积的最大值及此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
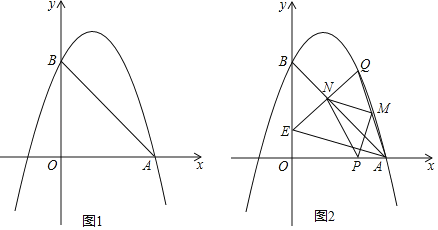
【题目】如图,抛物线y=﹣x2+bx+c与x轴正半轴交于A点,与y轴正半轴交于B,直线AB的解析式为y=﹣x+3.
(1)求抛物线解析式;
(2)P为线段OA上一点(不与O、A重合),过P作PQ⊥x轴交抛物线于Q,连接AQ,M为AQ中点,连接PM,过M作MN⊥PM交直线AB于N,若点P的横坐标为t,点N的横坐标为n,求n与t的函数关系式;
(3)在(2)的条件下,连接QN并延长交y轴于E,连接AE,求t为何值时,MN∥AE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“安全教育平台”是中国教育学会为方便学长和学生参与安全知识活动、接受安全提醒的一种应用软件.某校为了了解家长和学生参与“防溺水教育”的情况,在本校学生中随机抽取部分学生作调查,把收集的数据分为以下4类情形:A.仅学生自己参与;B.家长和学生一起参与;
C.仅家长自己参与; D.家长和学生都未参与.

请根据图中提供的信息,解答下列问题:
(1)在这次抽样调查中,共调查了________名学生;
(2)补全条形统计图,并在扇形统计图中计算C类所对应扇形的圆心角的度数;
(3)根据抽样调查结果,估计该校2000名学生中“家长和学生都未参与”的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com